题目内容
17.判断函数的奇偶性.(1)f(x)=(1+x)$\sqrt{\frac{1-x}{1+x}}$;
(2)f(x)=$\frac{\sqrt{1-{x}^{2}}}{|x+2|-2}$.
分析 根据奇函数和偶函数的定义,逐一分析各个函数是否满足定义,可得结论.
解答 解:(1)函数f(x)=(1+x)$\sqrt{\frac{1-x}{1+x}}$的定义域为(-1,1]不关于原点对称,
故)函数f(x)=(1+x)$\sqrt{\frac{1-x}{1+x}}$为非奇非偶函数;
(2)函数f(x)=$\frac{\sqrt{1-{x}^{2}}}{|x+2|-2}$的定义域为[-1,0)∪(0,1]关于原点对称,
且f(x)=$\frac{\sqrt{1-{x}^{2}}}{|x+2|-2}$=$\frac{\sqrt{1-{x}^{2}}}{x}$在定义域内满足f(-x)=-f(x)恒成立,是奇函数.
点评 本题考查的知识点是函数奇偶性的判定,熟练掌握并正确理解函数奇偶性的定义,是解答的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
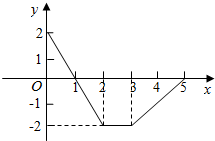 已知y=f(x)的图象如图所示.
已知y=f(x)的图象如图所示.