Question

13、已知函数y=x²-2|x|：（1）判断它的奇偶性；（2）画出函数的图象（3）根据图象写出单调递增区间

Answer 1

分析：（1）根据函数奇偶性的定义判断该函数的奇偶性是解决本题的关键，注明函数的定义域，判断f（-x）与f（x）的关系；
（2）根据函数奇偶性得出该函数的对称性，可以先画出该函数在（0，+∞）上的图象，利用对称性得出该函数在整个定义域上的图象；
（3）根据图象观察得出函数的单调增区间．

解答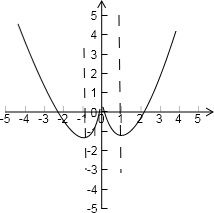：解：（1）由于该函数的定义域是R，
f（-x）=（-x）²-2|-x|═x²-2|x|=f（x），
故该函数是偶函数；
（2）由于该函数是偶函数，故其图象关于y轴对称，
当x≥0时，y=x²-2x，先画出该部分的图象，
利用对称性得出该函数的完整的图象．
（3）据图象写出该函数的单调递增区间为：（-1，0），（1，+∞）．

点评：本题考查函数奇偶性的应用问题，考查函数奇偶性的判断方法，考查函数图象的作法，考查数形结合思想和等价转化思想．关键要把握准函数图象的增减趋势．