题目内容
【题目】已知极坐标系的极点与直角坐标系的原点重合，极轴与x轴的非负半轴重合，若曲线C1的方程为ρsin（θ+ 
）+2 
=0，曲线C2的参数方程为 
（θ为参数）．
（1）将C1的方程化为直角坐标方程；
（2）若点Q为C2上的动点，P为C1上的动点，求|PQ|的最小值．
【答案】
（1）解：曲线C1的方程为ρsin（θ+ 
）+2 
=0，展开可得： 
+ 
+2 =0，可得直角标准方程： y+x+4 =0
（2）解：设点Q（2cosθ，2sinθ），则点Q到直线C1的距离d= 
= 
+2 ≥2 ﹣2，当且仅当 
=﹣1时取等号．
∴|PQ|的最小值为2 ﹣2
【解析】（1）曲线C1的方程为ρsin（θ+ ）+2 =0，展开可得： + +2 =0，利用 
代入即可得出直角标准方程．（2）设点Q（2cosθ，2sinθ），可得点Q到直线C1的距离d= +2 ，利用三角函数的单调性值域即可得出最小值．
手拉手全优练考卷系列答案【题目】某市为提高市民的戒烟意识，通过一个戒烟组织面向全市烟民征招志愿戒烟者，从符合条件的志愿者中随机抽取100名，将年龄分成
，
，
，
，
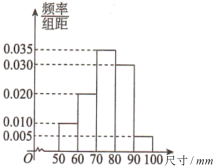
五组，得到频率分布直方图如图所示.
（1）求图中
的值，并估计这100名志愿者的平均年龄（同一组中的数据用该组区间的中点值作代表）；
（2）若年龄在的志愿者中有2名女性烟民，现从年龄在的志愿者中随机抽取2人，求至少有一名女性烟民的概率；
（3）该戒烟组织向志愿者推荐了
，
两种戒烟方案，这100名志愿者自愿选取戒烟方案，并将戒烟效果进行统计如下：
有效 | 无效 | 合计 | |
方案 | 48 | 60 | |
方案 | 36 | ||
合计 |
完成上面的
列联表，并判断是否有
的把握认为戒烟方案是否有效与方案选取有关.
参考公式：
，
.
参考数据：
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
【题目】东莞市公交公司为了方便广大市民出行，科学规划公交车辆的投放，计划在某个人员密集流动地段增设一个起点站，为了研究车辆发车的间隔时间
与乘客等候人数
之间的关系，选取一天中的六个不同的时段进行抽样调查，经过统计得到如下数据：
间隔时间（ | 8 | 10 | 12 | 14 | 16 | 18 |
等候人数（ | 16 | 19 | 23 | 26 | 29 | 33 |
调查小组先从这6组数据中选取其中的4组数据求得线性回归方程，再用剩下的2组数据进行检验，检验方法如下：先用求得的线性回归方程计算间隔时间对应的等候人数
，再求与实际等候人数的差，若两组差值的绝对值均不超过1，则称所求的回归方程是“理想回归方程”.
参考公式：用最小二乘法求线性回归方程
的系数公式：
，
（1）若选取的是前4组数据，求关于的线性回归方程
；
（2）判断（1）中的方程是否是“理想回归方程”：
（3）为了使等候的乘客不超过38人，试用（1）中方程估计间隔时间最多可以设置为多少分钟？
