题目内容
设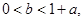 若关于
若关于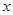 的不等式
的不等式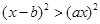 的解集中的整数恰有3个,则( )
的解集中的整数恰有3个,则( )
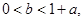 若关于
若关于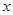 的不等式
的不等式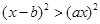 的解集中的整数恰有3个,则( )
的解集中的整数恰有3个,则( )A.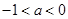 | B.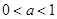 | C.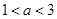 | D.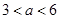 |
C
试题分析:要使关于x的不等式(x-b)2>(ax)2的解集中的整数恰有3个,那么此不等式的解集不能是无限区间,从而其解集必为有限区间,由题得不等式(x-b)2>(ax)2,即(a2-1)x2+2bx-b2<0,它的解应在两根之间,,因此应有 a2-1>0,解得a>1或a<-1,注意到0<b<1+a,从而a>1,,故有△=4b2+4b2(a2-1)=4a2b2>0,,不等式的解集为或者
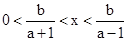
若不等式的解集为
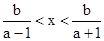 又由0<b<1+a得0<
又由0<b<1+a得0<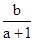 <1,
<1,故-3<
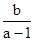 <-2,0<
<-2,0<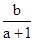 <1,这三个整数解必为-2,-1,0,2(a-1)<b≤3 (a-1),,注意到a>1,并结合已知条件0<b<1+a.,故要满足题设条件,只需要2(a-1)<1+a<3(a-1) 即可,则,b>2a-2,b<3a-3,又0<b<1+a,故 1+a>2a-2,3a-3>0解得1<a<3,综上1<a<3.故选C.
<1,这三个整数解必为-2,-1,0,2(a-1)<b≤3 (a-1),,注意到a>1,并结合已知条件0<b<1+a.,故要满足题设条件,只需要2(a-1)<1+a<3(a-1) 即可,则,b>2a-2,b<3a-3,又0<b<1+a,故 1+a>2a-2,3a-3>0解得1<a<3,综上1<a<3.故选C.点评:解决该试题的关键是对于二次不等式的开口方向和因式分解的正确处理。

练习册系列答案
相关题目
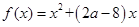 ,不等式
,不等式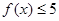 的解集是
的解集是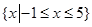 .
.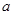 的值;
的值;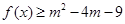 对于
对于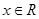 恒成立,求实数
恒成立,求实数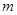 的取值范围.
的取值范围.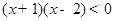 的解集为( )
的解集为( )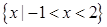
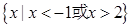
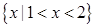
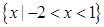
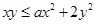 ,若对任意
,若对任意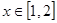 且
且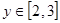 ,该不等式恒成立,则实数
,该不等式恒成立,则实数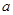 的取值范围是 .
的取值范围是 .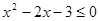 的解集是
的解集是  ,[0.5]=0,则使[x2-1]=3的x的取值范围是
,[0.5]=0,则使[x2-1]=3的x的取值范围是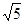 )
)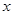 的不等式
的不等式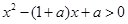 .
.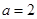 时,求不等式的解集;
时,求不等式的解集;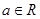 时,解不等式.
时,解不等式.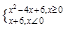 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( )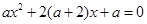 有实数解,那么实数a的取值范围是____________.
有实数解,那么实数a的取值范围是____________.