题目内容
已知x,y为正实数,满足1≤lg(xy)≤2,3≤lg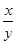 ≤4,求lg(x4y2)的取值范围.
≤4,求lg(x4y2)的取值范围.
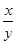 ≤4,求lg(x4y2)的取值范围.
≤4,求lg(x4y2)的取值范围.[6,10]
解:设a=lgx,b=lgy,则lg(xy)=a+b,
lg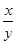 =a-b,lg(x4y2)=4a+2b,
=a-b,lg(x4y2)=4a+2b,
设4a+2b=m(a+b)+n(a-b),
∴ 解得
解得
又∵3≤3(a+b)≤6,3≤a-b≤4.
∴6≤4a+2b≤10.
即lg(x4y2)的取值范围为[6,10].
lg
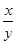 =a-b,lg(x4y2)=4a+2b,
=a-b,lg(x4y2)=4a+2b,设4a+2b=m(a+b)+n(a-b),
∴
 解得
解得
又∵3≤3(a+b)≤6,3≤a-b≤4.
∴6≤4a+2b≤10.
即lg(x4y2)的取值范围为[6,10].

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
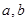 为非零实数,且
为非零实数,且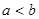 ,则下列命题成立的是( )
,则下列命题成立的是( )



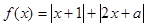 的最小值3,则实数
的最小值3,则实数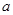 的值为( )
的值为( ) 或5
或5
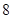
 的不等式
的不等式 的解集为
的解集为 ,则
,则 ________.
________. .
. ;
;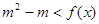 ,
,  都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 恒成立的是( )
恒成立的是( )



 满足
满足 ,则
,则 的取值范围是__________.
的取值范围是__________. 的不等式
的不等式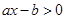 的解集是
的解集是 ,则关于
,则关于 的解( )
的解( )


