题目内容
 (2012•芜湖二模)如图,直角坐标系XOY中,点F在x轴正半轴上,△OFG的面积为S.且
(2012•芜湖二模)如图,直角坐标系XOY中,点F在x轴正半轴上,△OFG的面积为S.且| OF |
| FG |
| OF |
| 3 |
| 4 |
(1)以O为中心,F为焦点的椭圆E经过点G,求点G的纵坐标.
(2)在(1)的条件下,当|
| OG |
(3)在(2)的条件下,设点A、B分别为椭圆E的左、右顶点,点C是椭圆的下顶点,点P在椭圆E上(与点A、B均不重合),点D在直线PA上,若直线PB的方程为,且
| AP |
| CD |
分析:(1)设G(x0,y0),利用△OFG的面积S=
c•|y0|=
c即可求得点G的纵坐标;
(2)利用
•
=c(x0-c)=1,可求得x0=c+
,从而可求得|
|=
(c≥2),构造函数f(c)=c+
,利用其单调性质可求得当c=2时f(c)有最小值
,从而可求得G点坐标;
(3)由(2)知:A(-
,0),B(
,0),C(0,-
),由设P(x1,y1),可求得kAP•kBP=-
,继而可求得kAP=-
,再由
•
=0可求得kCD=5,从而可求得直线CD的方程.
| 1 |
| 2 |
| 3 |
| 4 |
(2)利用
| OF |
| FG |
| 1 |
| c |
| OG |
(c+
|
| 1 |
| c |
| 5 |
| 2 |
(3)由(2)知:A(-
| 10 |
| 10 |
| 6 |
| 3 |
| 5 |
| 1 |
| 5 |
| AP |
| CD |
解答:解:(1)设G(x0,y0)∵S=
|
|•|y0|,
∴
c=
c•|y0|,|y0|=
,
∵
=(c,0),
=(x0-c,y0)(y0>0),
∴y0=
…(3分)
(2)由(1)知
•
=c(x0-c)=1,∴x0=c+
∴|
|=
=
(c≥2)
∵f(c)=c+
在[2,+∞]上递增,
∴当c=2时f(c)有最小值2+
=
,
此时x0=
,y0=
,
∴G(
,
),
由于点G在椭圆E上,且c=2∴可求得a2=10,b2=6
方程为:
+
=1…(8分)
(3)由(2)知:A(-
,0),B(
,0),C(0,-
),
∵直线BP:y=kx-3
经过点B,
∴求得k=3
又设P(x1,y1)则y12=
(10-x12),
∴kAP•kBP=
×
=
=
=-
=-
,
∴kAP=-
×
=-
•
=-
•
=-
,
∵
•
=0,
∴kAP•kCD=-1,
∴-
•kCD=-1,
∴kCD=5.
又CD直线过点C(0,-
)故:所求CD方程为:y=5x-
…(13分)
| 1 |
| 2 |
| OF |
∴
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
∵
| OF |
| FG |
∴y0=
| 3 |
| 2 |
(2)由(1)知
| OF |
| FG |
| 1 |
| c |
∴|
| OG |
| x02+y02 |
(c+
|
∵f(c)=c+
| 1 |
| c |
∴当c=2时f(c)有最小值2+
| 1 |
| 2 |
| 5 |
| 2 |
此时x0=
| 5 |
| 2 |
| 3 |
| 2 |
∴G(
| 5 |
| 2 |
| 3 |
| 2 |
由于点G在椭圆E上,且c=2∴可求得a2=10,b2=6
方程为:
| x2 |
| 10 |
| y2 |
| 6 |
(3)由(2)知:A(-
| 10 |
| 10 |
| 6 |
∵直线BP:y=kx-3
| 10 |
∴求得k=3
| 10 |
又设P(x1,y1)则y12=
| 6 |
| 10 |
∴kAP•kBP=
| y1 | ||
x1-
|
| y1 | ||
x1+
|
| ||
|
=
| ||||
|
| 6 |
| 10 |
| 3 |
| 5 |
∴kAP=-
| 3 |
| 5 |
| 1 |
| kBP |
| 3 |
| 5 |
| 1 |
| k |
| 3 |
| 5 |
| 1 |
| 3 |
| 1 |
| 5 |
∵
| AP |
| CD |
∴kAP•kCD=-1,
∴-
| 1 |
| 5 |
∴kCD=5.
又CD直线过点C(0,-
| 6 |
| 6 |
点评:本题考查椭圆的标准方程,考查直线与圆锥曲线的关系的综合应用,考查双钩函数的单调性与最值,考查综合分析与应用的能力,属于难题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
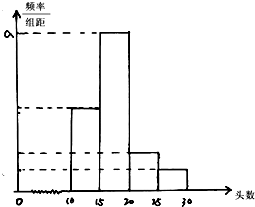 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: