题目内容
设函数 ,
,
(1)求函数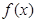 的极大值;
的极大值;
(2)记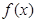 的导函数为
的导函数为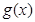 ,若
,若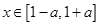 时,恒有
时,恒有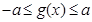 成立,试确定实数
成立,试确定实数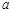 的取值范围.
的取值范围.
(1) ;(2)
;(2)  .
.
解析试题分析:(1)由导函数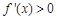 或
或 求得函数的单调区间,再找极大值;(2)
求得函数的单调区间,再找极大值;(2) 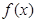 的导函数
的导函数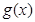 是一元二次函数,转化为一元二次函数在
是一元二次函数,转化为一元二次函数在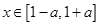 上的最值,再满足
上的最值,再满足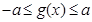 条件即可.
条件即可.
试题解析:(1)令 ,且
,且
当 时,得
时,得 ;当
;当 时,得
时,得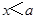 或
或
∴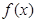 的单调递增区间为
的单调递增区间为 ;
;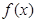 的单调递减区间为
的单调递减区间为 和
和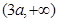 ,
,
故当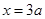 时,
时,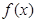 有极大值,其极大值为
有极大值,其极大值为 6分
6分
(2)∵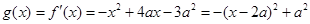 7分
7分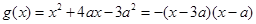
①当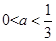 时,
时,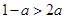 ,∴
,∴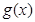 在区间
在区间 内单调递减
内单调递减
∴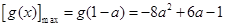 ,且
,且
∵恒有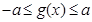 成立
成立
∵ 又
又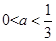 ,此时,
,此时, 10分
10分
②当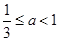 时,
时, ,得
,得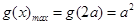
因为恒有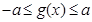 成立,所以
成立,所以 ,即
,即 ,又
,又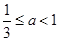
得 , 14分
, 14分
综上可知,实数 的取值范围
的取值范围 . 15分
. 15分
考点:1.函数的极值;2.一元二次函数的最值.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 (
( 且
且 )
) 的单调性;
的单调性; ,证明:
,证明: 时,
时, 成立
成立 .
. 的单调性;
的单调性; 恒成立,证明:当
恒成立,证明:当 时,
时, .
. (
( ).
). 的单调区间;
的单调区间; (
( )的单调性证明:当
)的单调性证明:当 时,
时, ;
; ,且
,且 均为正实数,
均为正实数,  时,
时, .
. -
-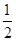 alnx,a∈R.
alnx,a∈R. )≤
)≤ ≤φ′(
≤φ′( ).
). ,
,
 .
. ,求函数
,求函数 在区间
在区间 上的最值;
上的最值; 恒成立,求
恒成立,求 的取值范围.
的取值范围. 是自然对数的底数
是自然对数的底数 ,
, ,且函数
,且函数 在点
在点 处的切线方程为
处的切线方程为 .
. ,当
,当 时,直线
时,直线 的斜率恒小于
的斜率恒小于 ,试求实数
,试求实数 .
. .
. 的极大值.
的极大值. ,使
,使 ;
; 与
与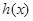 定义域内的任意实数x,若存在常数k,b,使得
定义域内的任意实数x,若存在常数k,b,使得 和
和 都成立,则称直线
都成立,则称直线 为函数
为函数
 的最小值
的最小值 的最小值C
的最小值C 若对于任意的
若对于任意的 ,恒有
,恒有 成立,求
成立,求 的取值范围.
的取值范围.