题目内容
如图,在底面为直角梯形的四棱锥S—ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=2AD.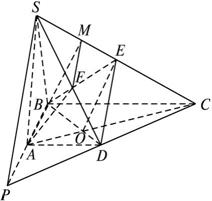
(1)求证:BC⊥平面SAB.
(2)求平面SCD与平面SAB所成二面角的正弦值.
(3)若E为SC上异于S、C的任意一点,问在SD上是否存在一点F,使AF∥平面BED?试说明理由.
(1)证明:∵SA⊥面ABCD,
∴SA⊥BC.
∵∠ABC=90°,∴AB⊥BC.
故BC⊥平面SAB.
(2)解:延长CD、BA交于点P,连结SP,
则SP为平面SCD与平面SAB的交线.
由条件计算可得∠BSP=90°,
由(1)BC⊥平面SAB,故SC⊥SP.
∴∠CSB就是平面SCD与平面SAB所成的二面角的平面角.
在Rt△CSB中,sin∠CSB=![]() .
.

∴平面SCD与平面SAB所成的二面角的正弦值为![]() .
.
(3)解:在SD上存在点F,使得AF∥平面BED.
连结AC与BD交于点O,连结OE,
在△SAC中,过点A作AM∥OE交SC于点M,
在△SDC中过点M作ED的平行线与SD交于F,连结AF,
则面AMF∥面EBD.
又AF![]() 平面AMF,故AF∥平面BED.
平面AMF,故AF∥平面BED.
∴在SD上存在一点F,使AF∥平面BED.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1, 如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点. 如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
