题目内容
已知,以点C(t, )为圆心的圆与x轴交于O、A两点,与y轴交于O、B两点.
)为圆心的圆与x轴交于O、A两点,与y轴交于O、B两点.(1)求证:S△AOB为定值;
(2)设直线y=-2x+4(3)与圆C交于点M、N,若OM=ON,求圆C的方程.
【答案】分析:(1)易得C(t, )为AB中点,从而可得A(2t,0),B(0,
)为AB中点,从而可得A(2t,0),B(0, ),由此可求S△AOB;
),由此可求S△AOB;
(2)kOC•kMN=-1,可得t=±2,从而可确定圆心与半径,再验证,当圆心C为(-2,-1)时,直线y=-2x+4与圆C相离,即可得到圆C的方程.
解答: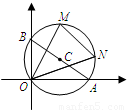 (1)证明:∵∠AOB=90°,
(1)证明:∵∠AOB=90°,
∴C(t, )为AB中点
)为AB中点
∴A(2t,0),B(0, )
)
∴S△AOB=
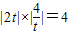
(2)解:∵OM=ON
∴O在线段MN的中垂线上
∴OC⊥MN
∴kOC•kMN=-1
∴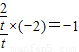
∴t=±2
∴圆心C(2,1)或(-2,-1),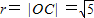
经验证,当圆心C为(-2,-1)时,直线y=-2x+4与圆C相离
∴圆C的方程为(x-2)2+(y-1)2=5
点评:本题考查圆方程的综合运用,考查求圆的方程,关键是确定圆的圆心与半径.
 )为AB中点,从而可得A(2t,0),B(0,
)为AB中点,从而可得A(2t,0),B(0, ),由此可求S△AOB;
),由此可求S△AOB;(2)kOC•kMN=-1,可得t=±2,从而可确定圆心与半径,再验证,当圆心C为(-2,-1)时,直线y=-2x+4与圆C相离,即可得到圆C的方程.
解答:
 (1)证明:∵∠AOB=90°,
(1)证明:∵∠AOB=90°,∴C(t,
 )为AB中点
)为AB中点∴A(2t,0),B(0,
 )
)∴S△AOB=

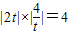
(2)解:∵OM=ON
∴O在线段MN的中垂线上
∴OC⊥MN
∴kOC•kMN=-1
∴
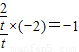
∴t=±2
∴圆心C(2,1)或(-2,-1),
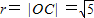
经验证,当圆心C为(-2,-1)时,直线y=-2x+4与圆C相离
∴圆C的方程为(x-2)2+(y-1)2=5
点评:本题考查圆方程的综合运用,考查求圆的方程,关键是确定圆的圆心与半径.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 )为圆心的圆与x轴交于O、A两点,与y轴交于O、B两点.
)为圆心的圆与x轴交于O、A两点,与y轴交于O、B两点. 与圆C交于点M、N,若OM = ON,求圆C的方程.
与圆C交于点M、N,若OM = ON,求圆C的方程.