题目内容
下列说法中:
① 若 (其中
(其中 )是偶函数,则实数
)是偶函数,则实数 ;
;
②  既是奇函数又是偶函数;
既是奇函数又是偶函数;
③ 函数 的减区间是
的减区间是 ;
;
④ 已知 是定义在
是定义在 上的不恒为零的函数,且对任意的
上的不恒为零的函数,且对任意的 都满足
都满足
 ,则
,则 是奇函数。
是奇函数。
其中正确说法的序号是( )
A.①②④ B.①③④
C.②③④ D.①②③
【答案】
A
【解析】
试题分析:① 若 (其中
(其中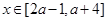 )是偶函数,则
)是偶函数,则 ,所以实数
,所以实数 ;
;
②  的定义域为{-2013,2013},所以
的定义域为{-2013,2013},所以 =0,所以既是奇函数又是偶函数;
=0,所以既是奇函数又是偶函数;
③ 函数 的减区间是
的减区间是 ;
;
④令  ,则
,则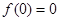 ;令
;令 ,则
,则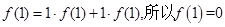 ;
;
令 ,
, ,所以
,所以 ;
;
令 ,则
,则 ,所以
,所以 是奇函数。
是奇函数。
考点:函数的奇偶性;复合函数的单调性;抽象函数的有关问题。
点评:此题考查的知识点较多,较为综合,属于中档题。①切记:偶函数的定义域一定关于原点对称。②判断函数的奇偶性,可以根据定义域先化简。③求函数的单调区间时,一定要先求函数的定义域。④有关抽象函数的问题,常用赋值法。

练习册系列答案
相关题目