题目内容
(2009湖南卷文)(本小题满分12分)
如图3,在正三棱柱![]() 中,AB=4,
中,AB=4, ![]() ,点D是BC的中点,点E在AC上,且DE
,点D是BC的中点,点E在AC上,且DE![]()
![]() E.
E.
(Ⅰ)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求直线AD和平面![]() 所成角的正弦值。
所成角的正弦值。

解析:(Ⅰ)如图所示,由正三棱柱![]() 的性质知
的性质知![]()
![]() 平面
平面![]() .
.
又DE![]() 平面ABC,所以DE
平面ABC,所以DE![]() .而DE
.而DE![]()
![]() E,
E,![]() ,
,
所以DE⊥平面![]() .又DE
.又DE ![]() 平面
平面![]() ,
,
故平面![]() ⊥平面
⊥平面![]() .
.
(Ⅱ)解法 1: 过点A作AF垂直![]() 于点
于点![]() ,
,
连接DF.由(Ⅰ)知,平面![]() ⊥平面
⊥平面![]() ,
,
所以AF![]() 平面
平面![]() ,故
,故![]() 是直线AD和
是直线AD和
平面![]() 所成的角。 因为DE
所成的角。 因为DE![]()
![]() ,
,
所以DE![]() AC.而
AC.而![]() ABC是边长为4的正三角形,
ABC是边长为4的正三角形,
于是AD=![]() ,AE=4-CE=4-
,AE=4-CE=4-![]() =3.
=3.
又因为![]() ,所以
,所以![]() E=
E= ![]()
![]() = 4,
= 4, ![]()
![]()
![]() ,
, ![]() .
.
即直线AD和平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
解法2 : 如图所示,设O是AC的中点,以O为原点建立空间直角坐标系,
则相关各点的坐标分别是A(2,0,0,), ![]() (2,0,
(2,0,![]() ), D(-1,
), D(-1, ![]() ,0), E(-1,0,0).
,0), E(-1,0,0).
易知![]() =(-3,
=(-3,![]() ,-
,-![]() ),
),![]() =(0,-
=(0,-![]() ,0),
,0),![]() =(-3,
=(-3,![]() ,0).
,0).
设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则

解得![]() .
.
故可取![]() .于是
.于是
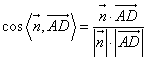 =
=![]() .
. ![]()
![]()
由此即知,直线AD和平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目

