题目内容
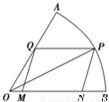
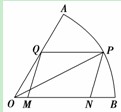
如图,现在要在一块半径为1m.圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设∠BOP=θ.平行四边形MNPQ的面积为S.(1)求S关于θ的函数关系式;
(2)求S的最大值及相应θ的值.
【答案】分析:(1)根据题设条件合理建立方程,从而导出S关于θ的函数关系式.
(2)利用三角函数求出S的最大值及相应θ的值.
解答:解:①分别过点P、Q作PD⊥OB,QE⊥OB,垂足分别为D、E,则四边形QEDP是矩形.
PD=sinθ,OD=cosθ.
在Rt△OEQ中,∠AOB=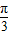 ,
,
则OE=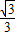 QE=
QE=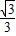 PD.
PD.
所以MN=PQ=DE=OD-OE=cosθ-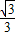 sinθ.
sinθ.
则S=MN×PD=(cosθ-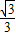 sinθ)×sinθ=sinθcosθ-
sinθ)×sinθ=sinθcosθ-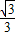 sin2θ,θ∈(0,
sin2θ,θ∈(0,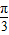 ).
).
(2)S= sin2θ-
sin2θ-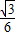 (1-cos2θ)=
(1-cos2θ)= sin2θ+
sin2θ+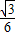 cos2θ-
cos2θ-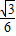 =
=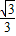 sin(2θ+
sin(2θ+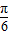 )-
)-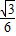 .
.
因为0<θ<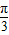 ,所以
,所以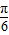 <2θ+
<2θ+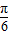 <
<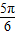 ,
,
所以 <sin(2θ+
<sin(2θ+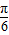 )≤1.所以当2θ+
)≤1.所以当2θ+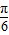 =
=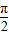 ,即θ=
,即θ=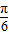 时,S的值最大为
时,S的值最大为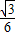 m2.
m2.
即S的最大值是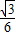 m2,相应θ的值是
m2,相应θ的值是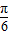 .
.
点评:挖掘题设条件,合理运用三角函数是正确解题的关键.
(2)利用三角函数求出S的最大值及相应θ的值.
解答:解:①分别过点P、Q作PD⊥OB,QE⊥OB,垂足分别为D、E,则四边形QEDP是矩形.
PD=sinθ,OD=cosθ.
在Rt△OEQ中,∠AOB=
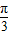 ,
,则OE=
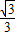 QE=
QE=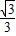 PD.
PD.所以MN=PQ=DE=OD-OE=cosθ-
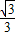 sinθ.
sinθ.则S=MN×PD=(cosθ-
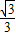 sinθ)×sinθ=sinθcosθ-
sinθ)×sinθ=sinθcosθ-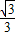 sin2θ,θ∈(0,
sin2θ,θ∈(0,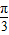 ).
).(2)S=
 sin2θ-
sin2θ-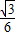 (1-cos2θ)=
(1-cos2θ)= sin2θ+
sin2θ+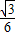 cos2θ-
cos2θ-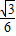 =
=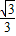 sin(2θ+
sin(2θ+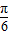 )-
)-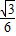 .
.因为0<θ<
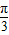 ,所以
,所以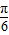 <2θ+
<2θ+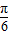 <
<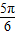 ,
,所以
 <sin(2θ+
<sin(2θ+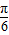 )≤1.所以当2θ+
)≤1.所以当2θ+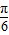 =
=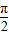 ,即θ=
,即θ=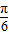 时,S的值最大为
时,S的值最大为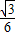 m2.
m2.即S的最大值是
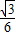 m2,相应θ的值是
m2,相应θ的值是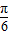 .
.点评:挖掘题设条件,合理运用三角函数是正确解题的关键.

练习册系列答案
相关题目
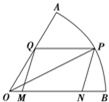 如图,现在要在一块半径为1m.圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设∠BOP=θ.平行四边形MNPQ的面积为S.
如图,现在要在一块半径为1m.圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设∠BOP=θ.平行四边形MNPQ的面积为S.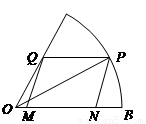
 的
的 的函数关系式;
的函数关系式;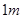 ,圆心角为
,圆心角为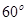 的扇形纸板
的扇形纸板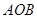 上剪出一个平行四边形
上剪出一个平行四边形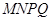 ,使点
,使点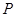 在弧
在弧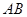 上,点
上,点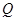 在
在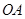 上,点
上,点 ,
, 在
在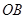 上,设
上,设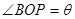 ,
,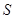 .
. 
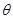 的函数关系式;
的函数关系式;