题目内容
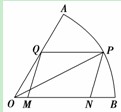
(12)如图,现在要在一块半径为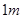 ,圆心角为
,圆心角为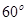 的扇形纸板
的扇形纸板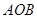 上剪出一个平行四边形
上剪出一个平行四边形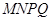 ,使点
,使点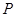 在弧
在弧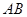 上,点
上,点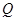 在
在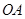 上,点
上,点 ,
, 在
在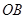 上,设
上,设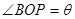 ,
,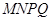 的面积为
的面积为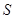 .
.
(1)求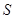 关于
关于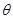 的函数关系式;
的函数关系式;
(2)求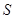 的最大值及相应
的最大值及相应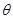 的值.
的值.
【答案】
①分别过点P、Q作PD⊥OB,QE⊥OB,垂足分别为D、E,则四边形QEDP是矩形.
PD=sinθ,OD=cosθ.
在Rt△OEQ中,∠AOB=,
则OE=QE=PD.
所以MN=PQ=DE=OD-OE=cosθ-sinθ.
则S=MN×PD=(cosθ-sinθ)×sinθ=sinθcosθ-sin2θ,θ∈(0,).
(2)S=sin2θ-(1-cos2θ)=sin2θ+cos2θ-=sin(2θ+)-.
因为0<θ<,所以<2θ+<,
所以<sin(2θ+)≤1. 所以当2θ+=,即θ=时,S的值最大为 m2.
即S的最大值是 m2,相应θ的值是.
【解析】略

练习册系列答案
相关题目

 (12)如图,现在要在一块半径为
(12)如图,现在要在一块半径为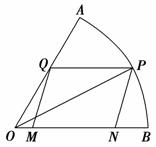 (1)求S关于θ的函数关系式;
(1)求S关于θ的函数关系式;