题目内容
【题目】综合题。
(1)利用“五点法”画出函数 ![]() 在
在 ![]() 内的简图
内的简图
x | |||||
| |||||
y |

(2)若对任意x∈[0,2π],都有f(x)﹣3<m<f(x)+3恒成立,求m的取值范围.
【答案】
(1)解:根据题意,函数 ![]() 在
在 ![]() 内的列表如下:
内的列表如下:
x |
|
|
|
|
|
| 0 |
| π |
| 2π |
y | 0 | 1 | 0 | ﹣1 | 0 |
在平面直角坐标系内可得图象如下:
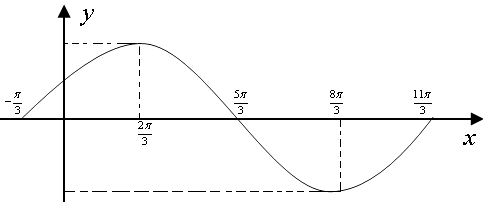
(2)解:通过图象可知:当x∈[0,2π]时,函f(x)值域为 ![]() ,
,
要使f(x)﹣3<m<f(x)+3恒成立,
即: 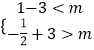
解得: ![]() ,
,
∴m的取值范围是 ![]() .
.
【解析】(1)根据列表、描点、连线的基本步骤,画出函数在一个周期在 ![]() 的大致图象即可.(2)根据x∈[0,2π],求解f(x)的值域,要使f(x)﹣3<m<f(x)+3恒成立,转化为最小和最大值问题.
的大致图象即可.(2)根据x∈[0,2π],求解f(x)的值域,要使f(x)﹣3<m<f(x)+3恒成立,转化为最小和最大值问题.
【考点精析】解答此题的关键在于理解五点法作函数y=Asin(ωx+φ)的图象的相关知识,掌握描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线).

练习册系列答案
相关题目