题目内容
（12分）
ABC中，a，b，c分别为内角A，B，C所对的边长，a=
，b=
，
，求边BC上的高.
ABC中，a，b，c分别为内角A，B，C所对的边长，a=，b=，，求边BC上的高.解：∵A＋B＋C＝180°，所以B＋C＝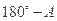
，
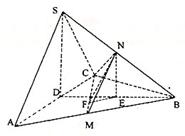
又，∴
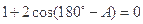
即
，
，
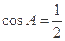又0°<A<180°，所以A＝60°.
在△ABC中，由正弦定理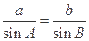
得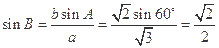
又∵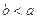
，所以B＜A，B＝45°，C＝75°，
∴BC边上的高AD＝AC·sinC＝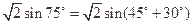
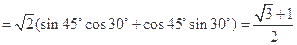
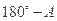，又
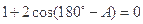
，∴ 即
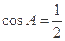，，又0°<A<180°，所以A＝60°.
在△ABC中，由正弦定理
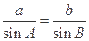得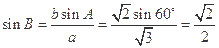又∵
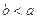，所以B＜A，B＝45°，C＝75°，∴BC边上的高AD＝AC·sinC＝
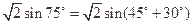
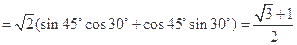
略
练习册系列答案
每课必练系列答案
相关题目
，
，则A=（ ）
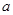，b，c，若
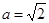，b=2，sinB+cosB=
，
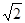中，已知
，
，
，则
，② 三根细钢管相交处的节点
与凳面三角形
重心的连线垂直于凳面和地面. （1）若凳面是边长为
的正三角形，三只凳脚与地面所成的角均为
，确定节点
的等腰三角形，腰长为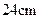
，节点
. 确定三根细钢管的长度.
中，侧面
与侧面
均是边长为
的正
，
是
的中点，
平面
;
的余弦值
中，
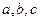分别为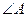
．
．
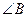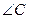的对边，已知
，
，
．
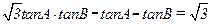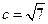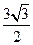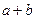的值．
的最小值为 ；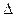
ABC的内角A，B，C的对边分别为a,b,c,且
_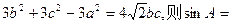