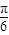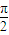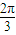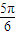题目内容
已知直线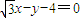 与圆x2+(y-2)2=25交于A、B两点,P为该圆上异于A、B的一动点,则△ABP的面积最大值是 .
与圆x2+(y-2)2=25交于A、B两点,P为该圆上异于A、B的一动点,则△ABP的面积最大值是 .
【答案】分析:根据题意可知且仅当p与AB之距离最大时,三角形ABP的面积最大,设:x=5cosa,y=2+5sina,进而根据点到直线的距离求得P到直线的距离表达式,进而根据三角函数的性质求得距离的最大值,进而根据弦长公式求得AB的长,则三角形面积可得.
解答:解:据平面几何知识知:当且仅当p与AB之距离最大时,三角形ABP的面积最大,设:x=5cosa,y=2+5sina,P(5cosa,2+5sina)与直线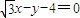 的距离得:d=
的距离得:d= |
|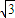 •5cosa-2-5sina-4|=
•5cosa-2-5sina-4|= |
|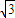 •5cosa-5sina-6|•≤
•5cosa-5sina-6|•≤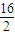 =8,又|AB|=2
=8,又|AB|=2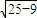 =8;
=8;
所以三角形ABP面积=8×8× =32
=32
故答案为32
点评:本题主要考查了直线与圆相交的性质.解题的关键是把问题转化成求得点到直线的距离最大值.
解答:解:据平面几何知识知:当且仅当p与AB之距离最大时,三角形ABP的面积最大,设:x=5cosa,y=2+5sina,P(5cosa,2+5sina)与直线
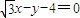 的距离得:d=
的距离得:d= |
|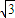 •5cosa-2-5sina-4|=
•5cosa-2-5sina-4|= |
|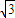 •5cosa-5sina-6|•≤
•5cosa-5sina-6|•≤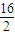 =8,又|AB|=2
=8,又|AB|=2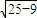 =8;
=8;所以三角形ABP面积=8×8×
 =32
=32故答案为32
点评:本题主要考查了直线与圆相交的性质.解题的关键是把问题转化成求得点到直线的距离最大值.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
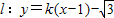 与圆x2+y2=1相切,则直线l的倾斜角为( )
与圆x2+y2=1相切,则直线l的倾斜角为( )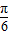
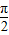
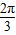
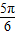
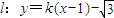 与圆x2+y2=1相切,则直线l的倾斜角为( )
与圆x2+y2=1相切,则直线l的倾斜角为( )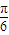
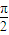
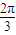
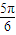
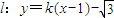 与圆x2+y2=1相切,则直线l的倾斜角为( )
与圆x2+y2=1相切,则直线l的倾斜角为( )