题目内容
已知函数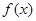 是定义在
是定义在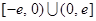 上的奇函数,当
上的奇函数,当 时,有
时,有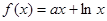 (其中
(其中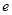 为自然对数的底,
为自然对数的底,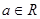 ).
).
(1)求函数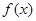 的解析式;
的解析式;
(2)设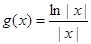 ,
, ,求证:当
,求证:当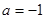 时,
时,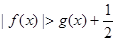 ;
;
(3)试问:是否存在实数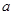 ,使得当
,使得当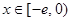 时,
时,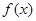 的最小值是3?如果存在,求出实数
的最小值是3?如果存在,求出实数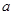 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(1)
(2)构造函数利用函数的最小值大于另一个函数的最大值来证明成立。
(3)当 时,函数
时,函数 在区间
在区间 上的最小值是3
上的最小值是3
【解析】
试题分析:解:(1)当 时,
时, ,
,
则 ,
,
又 是奇函数,
是奇函数,
所以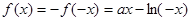 ,
,
因此, ;
4分
;
4分
(2)证明:令 ,
,
当 时,注意到
时,注意到 ,所以
,所以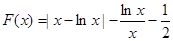
 5分
5分
① 当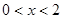 时,注意到
时,注意到 ,有
,有
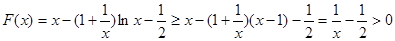 ;
6分
;
6分
② 当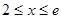 时,
时,
 , 7分
, 7分
故函数 在
在 上是增函数,从而有
上是增函数,从而有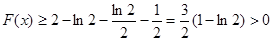 ,
,
所以当 时,有
时,有 ,
8分
,
8分
又因为 是偶函数,故当
是偶函数,故当 时,同样有
时,同样有 ,即
,即 ,
,
综上所述,当 时,有
时,有 ;
9分
;
9分
(2)证法二:当 时,
时, ,
,
求导得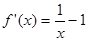 ,令
,令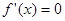 得
得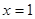 ,
5分
,
5分
于是可得当 时,
时, ;
; 时,
时, ,
,
所以 在
在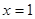 处取得最大值
处取得最大值 ,所以
,所以 .
6分
.
6分
又记 ,当
,当 时,有
时,有 ,
7分
,
7分
求导得 ,当
,当 时,
时, ,
,
所以 在
在 上单调递增,于是
上单调递增,于是 ,
,
所以,在在 上总有
上总有 .
8分
.
8分
注意到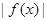 和
和 的偶函数性质,
的偶函数性质,
所以当 时,有
时,有 (
(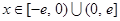 );
9分
);
9分
(3)当 时,
时, ,
,
求导得 ,令
,令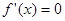 得
得 ,
10分
,
10分
① 当 时,
时, ,
, 在区间
在区间 上是增函数,故此时函数
上是增函数,故此时函数 在区间
在区间 上的最小值为
上的最小值为 ,不满足要求;
11分
,不满足要求;
11分
② 当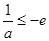 ,即
,即 时,
时, ,
,
所以 在区间
在区间 上是增函数,此时函数
上是增函数,此时函数 在区间
在区间 的最小值为
的最小值为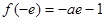 ,
,
令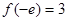 ,得
,得 ,也不满足要求;
12分
,也不满足要求;
12分
③ 当 时,可得
时,可得 在区间
在区间 上是减函数,在区间
上是减函数,在区间 上是增函数,所以当
上是增函数,所以当 时,
时, ,
,
令 ,得
,得 ,满足要求.
13分
,满足要求.
13分
综上可得,当 时,函数
时,函数 在区间
在区间 上的最小值是3. 14分
上的最小值是3. 14分
考点:导数的应用
点评:解决的关键是根据导数的符号于函数单调性的关系来判定单调性,进而得到最值,属于基础题

 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。 的解析式;
的解析式; 。
。 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式;
 是定义在
是定义在 上的以5为周期的奇函数, 若
上的以5为周期的奇函数, 若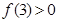 ,
, ,则a的取值范围是 ( )
,则a的取值范围是 ( )  B.
B.

 D.
D.

 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
) ,求证:当
,求证:当 时,
时, ;
; 时,
时, 是定义在
是定义在 上的奇函数,且
上的奇函数,且
 的解析式;
的解析式; 的单调性;
的单调性;