题目内容
【题目】已知数列{an}的首项a1=1,前n项和为Sn , 且满足(n+1)an=2Sn(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=ancos(πan),求数列{bn)的前n项和Tn .
【答案】
(1)解:∵(n+1)an=2Sn,∴(n+2)an+1=2Sn+1.
两式相减,得(n+1)an=nan+1,即 ![]() =
= ![]() .
.
∴an= ![]() …
… ![]()
= ![]() …
… ![]() ×1=n
×1=n
(2)解:∵bn=ancos(πan)=ncosnπ=n(﹣1)n,
∴Tn=1×(﹣1)+2×(﹣1)2+3×(﹣1)3+4×(﹣1)4+…+n×(﹣1)n,①
﹣Tn=1×(﹣1)2+2×(﹣1)3+3×(﹣1)4+4×(﹣1)5+…+n×(﹣1)n+1.②
①﹣②,整理得
2Tn=﹣1+(﹣1)2+(﹣1)3+(﹣1)4+…+(﹣1)n﹣n(﹣1)n+1= ![]() ﹣﹣n(﹣1)n+1
﹣﹣n(﹣1)n+1
∴Tn= ![]() (﹣1)n﹣
(﹣1)n﹣ ![]() .
.
【解析】解法2:bn=ancos(πan)=ncosnπ=n(﹣1)n= ![]() .
.
当n为偶数时,Tn=﹣1+2﹣3+4﹣5+6…﹣(n(n﹣1)﹣n= ![]() ﹣n=﹣
﹣n=﹣ ![]() .
.
∴Tn= ![]() (﹣1)n﹣
(﹣1)n﹣ ![]() .
.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系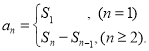 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

 阅读快车系列答案
阅读快车系列答案【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名六年级学生进行了问卷调查得到如图联表.且平均每天喝500ml以上为常喝,体重超过50kg为肥胖.已知在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8.
常喝 | 不常喝 | 合计 | |
肥胖 | 60 | ||
不肥胖 | 10 | ||
合计 | 100 |
(1)求肥胖学生的人数并将上面的列联表补充完整;
(2)是否有95%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由. 附:参考公式:x2= ![]()
P(x2≥x0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |