题目内容
已知a0≠0.
①设方程a0x+a1=0的1个根是x1,则x1=-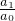 ;
;
②设方程a0x2+a1x+a2=0的2个根是x1,x2,则x1x2=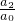 ;
;
③设方程a0x3+a1x2+a2x+a3=0的3个根是x1,x2,x3,则x1x2x3=-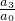 ;
;
④设方程a0x4+a1x3+a2x2+a3x+a4=0的4个根是x1,x2,x3,x4,则x1x2x3x4=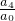 ;
;
…
由以上结论,推测出一般的结论:
设方程a0xn+a1xn-1+a2xn-2+…+an-1x+an=0的n个根是x1,x2,…,xn,
则x1x2…xn=________.
(-1)n
分析:解答此类的方法是从特殊的前几个式子进行分析找出规律.观察前几个式子的变化规律,发现每一个方程的一个根都可能写成规律性的式子,是首项与尾项的分式形式,且符号是正负相间.
解答:观察式子的变化规律,
发现每一个方程的一个根都可能写成规律性的式子,
是首项与尾项的分式形式,且符号是正负相间:
-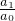 ;
;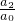 ;-
;-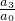 ;…
;…
依此类推,第n个式子是(-1)n .
.
故答案为:(-1)n .
.
点评:所谓归纳推理,就是从个别性知识推出一般性结论的推理.它与演绎推理的思维进程不同.归纳推理的思维进程是从个别到一般,而演绎推理的思维进程不是从个别到一般,是一个必然地得出的思维进程.

分析:解答此类的方法是从特殊的前几个式子进行分析找出规律.观察前几个式子的变化规律,发现每一个方程的一个根都可能写成规律性的式子,是首项与尾项的分式形式,且符号是正负相间.
解答:观察式子的变化规律,
发现每一个方程的一个根都可能写成规律性的式子,
是首项与尾项的分式形式,且符号是正负相间:
-
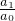 ;
;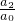 ;-
;-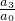 ;…
;…依此类推,第n个式子是(-1)n
 .
.故答案为:(-1)n
 .
.点评:所谓归纳推理,就是从个别性知识推出一般性结论的推理.它与演绎推理的思维进程不同.归纳推理的思维进程是从个别到一般,而演绎推理的思维进程不是从个别到一般,是一个必然地得出的思维进程.

练习册系列答案
相关题目
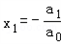 ,方程
,方程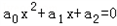 的两个根是x1,x2,则
的两个根是x1,x2,则 ,由此类推方程
,由此类推方程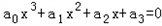 的三个根是x1,x2,x3,则x1+x2+x3=( )
的三个根是x1,x2,x3,则x1+x2+x3=( )