题目内容
已知函数f(x)=x+1,设g1(x)=f(x),gn(x)=f(gn-1(x))(n>1,n∈N*)(1)求g2(x),g3(x)的表达式,并猜想gn(x)(n∈N*)的表达式(直接写出猜想结果)
(2)若关于x的函数
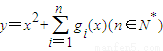 在区间(-∞,-1]上的最小值为6,求n的值.
在区间(-∞,-1]上的最小值为6,求n的值.(符号“
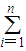 ”表示求和,例如:
”表示求和,例如: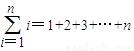 .)
.)
【答案】分析:(1)根据g1(x)=f(x),gn(x)=f(gn-1(x)),令n=2,3,即可求得求g2(x),g3(x)的表达式,并猜想gn(x)(n∈N*)的表达式;
(2)根据(1)的结果代入求出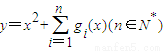 ,转化为二次函数利用配方法求最值,讨论对称轴是否在定义域内.
,转化为二次函数利用配方法求最值,讨论对称轴是否在定义域内.
解答:解:(1)∵g1(x)=f(x)=x+1,
∴g2(x)=f(g1(x))=f(x+1)=(x+1)+1=x+2,
g3(x)=f(g2(x))=f(x+2)=(x+2)+1=x+3,
∴猜想gn(x)=x+n
(2)∵gn(x)=x+n,
∴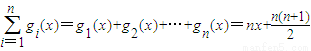
∴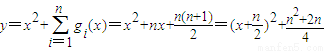
1°当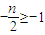 ,即n≤2时,函数
,即n≤2时,函数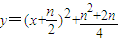 在区间(-∞,-1]上是减函数∴当x=-1时,
在区间(-∞,-1]上是减函数∴当x=-1时, ,即n2-n-10=0,该方程没有整数解
,即n2-n-10=0,该方程没有整数解
2°当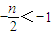 ,即n>2时,
,即n>2时,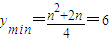 ,解得n=4,
,解得n=4,
综上所述,n=4
点评:此题是个中档题.考查代入法求函数的解析式、归纳法、和二次函数求最值的配方法等基本方法,体现了分类讨论的思想.很好的考查了学生的阅读能力和灵活应用知识分析解决问题的能力.
(2)根据(1)的结果代入求出
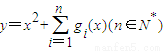 ,转化为二次函数利用配方法求最值,讨论对称轴是否在定义域内.
,转化为二次函数利用配方法求最值,讨论对称轴是否在定义域内.解答:解:(1)∵g1(x)=f(x)=x+1,
∴g2(x)=f(g1(x))=f(x+1)=(x+1)+1=x+2,
g3(x)=f(g2(x))=f(x+2)=(x+2)+1=x+3,
∴猜想gn(x)=x+n
(2)∵gn(x)=x+n,
∴
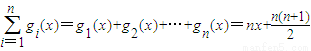
∴
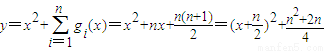
1°当
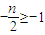 ,即n≤2时,函数
,即n≤2时,函数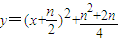 在区间(-∞,-1]上是减函数∴当x=-1时,
在区间(-∞,-1]上是减函数∴当x=-1时, ,即n2-n-10=0,该方程没有整数解
,即n2-n-10=0,该方程没有整数解2°当
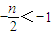 ,即n>2时,
,即n>2时,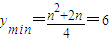 ,解得n=4,
,解得n=4,综上所述,n=4
点评:此题是个中档题.考查代入法求函数的解析式、归纳法、和二次函数求最值的配方法等基本方法,体现了分类讨论的思想.很好的考查了学生的阅读能力和灵活应用知识分析解决问题的能力.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|