题目内容
求下列函数的定义域及值域.
(1)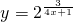 ;
;
(2)y=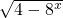 .
.
解:(1)要使函数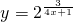 有意义,只需4x+1≠0,即x≠-
有意义,只需4x+1≠0,即x≠- ,
,
所以,函数的定义域为{x|x≠- }.
}.
设y=2u,u=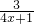 ≠0,则u>0,由函数y=2u,得y≠20=1,所以函数的值域为{y|0<y且y≠1}.
≠0,则u>0,由函数y=2u,得y≠20=1,所以函数的值域为{y|0<y且y≠1}.
(2)由4-8x≥0,得x≤ ,所以函数的定义域为{x|x
,所以函数的定义域为{x|x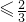 }.
}.
因0≤4-8x<4,所以0≤y<2,所以函数的值域为[0,2).
分析:(1)要使函数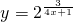 有意义,只需4x+1≠0,由此解得函数的定义域.根据u=
有意义,只需4x+1≠0,由此解得函数的定义域.根据u=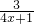 ≠0,由函数y=2u的性质得0<y≠20=1,得函数的值域.
≠0,由函数y=2u的性质得0<y≠20=1,得函数的值域.
(2)函数y=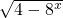 的被开方数为非负数,可得函数的定义域.由0≤4-8x<4,所以0≤y<2,此可得函数的值域.
的被开方数为非负数,可得函数的定义域.由0≤4-8x<4,所以0≤y<2,此可得函数的值域.
点评:本题主要考查求函数的定义域和值域,函数的单调性的应用,属于基础题.
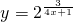 有意义,只需4x+1≠0,即x≠-
有意义,只需4x+1≠0,即x≠- ,
,所以,函数的定义域为{x|x≠-
 }.
}.设y=2u,u=
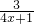 ≠0,则u>0,由函数y=2u,得y≠20=1,所以函数的值域为{y|0<y且y≠1}.
≠0,则u>0,由函数y=2u,得y≠20=1,所以函数的值域为{y|0<y且y≠1}.(2)由4-8x≥0,得x≤
 ,所以函数的定义域为{x|x
,所以函数的定义域为{x|x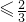 }.
}.因0≤4-8x<4,所以0≤y<2,所以函数的值域为[0,2).
分析:(1)要使函数
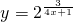 有意义,只需4x+1≠0,由此解得函数的定义域.根据u=
有意义,只需4x+1≠0,由此解得函数的定义域.根据u=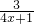 ≠0,由函数y=2u的性质得0<y≠20=1,得函数的值域.
≠0,由函数y=2u的性质得0<y≠20=1,得函数的值域.(2)函数y=
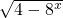 的被开方数为非负数,可得函数的定义域.由0≤4-8x<4,所以0≤y<2,此可得函数的值域.
的被开方数为非负数,可得函数的定义域.由0≤4-8x<4,所以0≤y<2,此可得函数的值域.点评:本题主要考查求函数的定义域和值域,函数的单调性的应用,属于基础题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 )6+x-2x2;
)6+x-2x2; )-|x|.
)-|x|.