题目内容
求下列函数的定义域及值域．
（1）y=2
；
（2）y=
．
（1）y=2
| 3 |
| 4x+1 |
（2）y=
| 4-8x |
（1）要使函数y=2
有意义，只需4x+1≠0，即x≠-
，
所以，函数的定义域为{x|x≠-
}．
设y=2u，u=
≠0，则u＞0，由函数y=2u，得y≠20=1，所以函数的值域为{y|0＜y且y≠1}．
（2）由4-8x≥0，得x≤
，所以函数的定义域为{x|x≤
}．
因0≤4-8x＜4，所以0≤y＜2，所以函数的值域为[0，2）．
| 3 |
| 4x+1 |
| 1 |
| 4 |
所以，函数的定义域为{x|x≠-
| 1 |
| 4 |
设y=2u，u=
| 3 |
| 4x+1 |
（2）由4-8x≥0，得x≤
| 2 |
| 3 |
| 2 |
| 3 |
因0≤4-8x＜4，所以0≤y＜2，所以函数的值域为[0，2）．
练习册系列答案
相关题目
； 
．
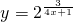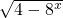）6+x-2x2；
）-|x|．