题目内容
设m、t为实数,函数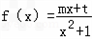 ,f(x)的图象在点M(0,f(0))处的切线的斜率为1.
,f(x)的图象在点M(0,f(0))处的切线的斜率为1.
(1)求实数m的值;
(2)若对于任意x∈[﹣1,2],总存在t,使得不等式f(x)≤2t成立,求实数t的取值范围;设方程x2+2tx﹣1=0的两个实数根为a,b(a<b),若对于任意x∈[a,b],总存在x1、x2∈[a,b],使得f(x1)≤f(x)≤f(x2)恒成立,记g(t)=f(x2)﹣f(x1),当 时,求实数t的值.
时,求实数t的值.
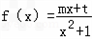 ,f(x)的图象在点M(0,f(0))处的切线的斜率为1.
,f(x)的图象在点M(0,f(0))处的切线的斜率为1.(1)求实数m的值;
(2)若对于任意x∈[﹣1,2],总存在t,使得不等式f(x)≤2t成立,求实数t的取值范围;设方程x2+2tx﹣1=0的两个实数根为a,b(a<b),若对于任意x∈[a,b],总存在x1、x2∈[a,b],使得f(x1)≤f(x)≤f(x2)恒成立,记g(t)=f(x2)﹣f(x1),当
 时,求实数t的值.
时,求实数t的值.解:(1)∵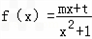
∴f '(x)=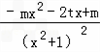
∵函数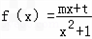 ,f(x)的图象在点M(0,f(0))处的切线的斜率为1
,f(x)的图象在点M(0,f(0))处的切线的斜率为1
∴f '(0)=1
∴m=1
(2)由(1)知f(x)=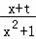
∵对于任意x∈[﹣1,2],总存在t,使得不等式f(x)≤2t成立
∴对于任意x∈[﹣1,2],总存在t,使得不等式t≥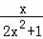 成立
成立
即t≥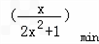
令s(x)=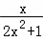 则s '(x)=
则s '(x)=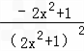
∴当s'(x)≥0时﹣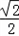 ≤x≤
≤x≤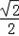
当s'(x)≤0时x≤﹣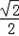 或x≥
或x≥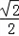 而x∈[﹣1,2]
而x∈[﹣1,2]
故﹣1≤x≤﹣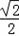 或
或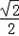 ≤x≤2
≤x≤2
∴s(x)在[﹣1,﹣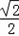 ]单调递减,在(﹣
]单调递减,在(﹣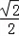 ,
,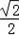 )单调递增,在[
)单调递增,在[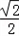 ,2]单调递减
,2]单调递减
∵s(﹣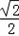 )=﹣
)=﹣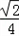 ,s(2)=
,s(2)=
∴s(x)min=﹣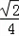
∴t≥﹣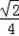
又由韦达定理可得a+b=﹣2t,ab=﹣1,b﹣a=2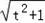
若对于任意x∈[a,b],总存在x1,x2∈[a,b]使得f(x1)≤f(x)≤f(x2)恒成立,说明x1,x2分别是区间[a,b]f(x)的最小最大值点.
由(1)可得,f'(x)=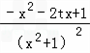 ,
,
注意h(x)=x2+2tx﹣1,不难发现函数f(x)在区间[a,b]f '(x)≥0,f(x)递增,
则x1=a,x2=b
则g(t)=f(x2)﹣f(x1)=f(b)﹣f(a)
=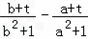 =
=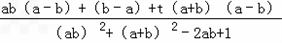
∵a+b=﹣2t,ab=﹣1,b﹣a=2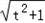
∴g(t)=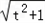
∵
∴t=±2
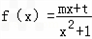
∴f '(x)=
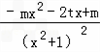
∵函数
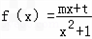 ,f(x)的图象在点M(0,f(0))处的切线的斜率为1
,f(x)的图象在点M(0,f(0))处的切线的斜率为1∴f '(0)=1
∴m=1
(2)由(1)知f(x)=
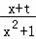
∵对于任意x∈[﹣1,2],总存在t,使得不等式f(x)≤2t成立
∴对于任意x∈[﹣1,2],总存在t,使得不等式t≥
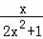 成立
成立即t≥
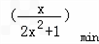
令s(x)=
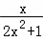 则s '(x)=
则s '(x)=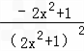
∴当s'(x)≥0时﹣
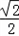 ≤x≤
≤x≤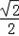
当s'(x)≤0时x≤﹣
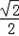 或x≥
或x≥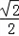 而x∈[﹣1,2]
而x∈[﹣1,2]故﹣1≤x≤﹣
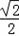 或
或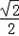 ≤x≤2
≤x≤2∴s(x)在[﹣1,﹣
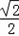 ]单调递减,在(﹣
]单调递减,在(﹣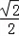 ,
,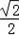 )单调递增,在[
)单调递增,在[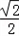 ,2]单调递减
,2]单调递减∵s(﹣
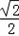 )=﹣
)=﹣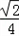 ,s(2)=
,s(2)=
∴s(x)min=﹣
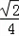
∴t≥﹣
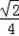
又由韦达定理可得a+b=﹣2t,ab=﹣1,b﹣a=2
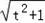
若对于任意x∈[a,b],总存在x1,x2∈[a,b]使得f(x1)≤f(x)≤f(x2)恒成立,说明x1,x2分别是区间[a,b]f(x)的最小最大值点.
由(1)可得,f'(x)=
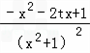 ,
,注意h(x)=x2+2tx﹣1,不难发现函数f(x)在区间[a,b]f '(x)≥0,f(x)递增,
则x1=a,x2=b
则g(t)=f(x2)﹣f(x1)=f(b)﹣f(a)
=
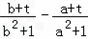 =
=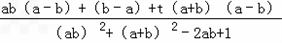
∵a+b=﹣2t,ab=﹣1,b﹣a=2
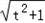
∴g(t)=
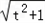
∵

∴t=±2

练习册系列答案
相关题目