题目内容
设m、t为实数,函数f(x)=
,f(x)的图象在点M(0,f(0))处的切线的斜率为1.
(1)求实数m的值;
(2)若对于任意x∈[-1,2],总存在t,使得不等式f(x)≤2t成立,求实数t的取值范围;设方程x2+2tx-1=0的两个实数根为a,b(a<b),若对于任意x∈[a,b],总存在x1、x2∈[a,b],使得f(x1)≤f(x)≤f(x2)恒成立,记g(t)=f(x2)-f(x1),当g(t)=
时,求实数t的值.
| mx+t |
| x2+1 |
(1)求实数m的值;
(2)若对于任意x∈[-1,2],总存在t,使得不等式f(x)≤2t成立,求实数t的取值范围;设方程x2+2tx-1=0的两个实数根为a,b(a<b),若对于任意x∈[a,b],总存在x1、x2∈[a,b],使得f(x1)≤f(x)≤f(x2)恒成立,记g(t)=f(x2)-f(x1),当g(t)=
| 5 |
分析:(1)根据导数的几何意义可得f′(0)=1即可求出m的值.
(2)根据f(x)=
可得t≥
成立即t≥(
)min从而将问题转化为求函数s(x)=
的最小值者可利用导数判断函数的单调性解决.而对于第二小问可根据对于任意x∈[a,b],总存在x1,x2∈[a,b]使得f(x1)≤f(x)≤f(x2)恒成立得出x1,x2分别是区间[a,b]f(x)的最小最大值点,然后利用导数求出函数f(x)的最大值点再代入到g(t)中结合a,b为方程x2+2tx-1=0的两个实数根即可得解.
(2)根据f(x)=
| x+t |
| x2+1 |
| x |
| 2x2+1 |
| x |
| 2x2+1 |
| x |
| 2x2+1 |
解答:解:(1)∵f(x)=
∴f′(x)=
∵函数f(x)=
,f(x)的图象在点M(0,f(0))处的切线的斜率为1
∴f′(0)=1
∴m=1
(2)由(1)知f(x)=
∵对于任意x∈[-1,2],总存在t,使得不等式f(x)≤2t成立
∴对于任意x∈[-1,2],总存在t,使得不等式t≥
成立即t≥(
)min
令s(x)=
则s′(x)=
∴当s′(x)≥0时-
≤x≤
当s′(x)≤0时x≤-
或x≥
而x∈[-1,2]故-1≤x≤-
或
≤x≤2
∴s(x)在[-1,-
]单调递减,在(-
,
)单调递增,在[
,2]单调递减
∵s(-
)=-
,s(2)=
∴s(x)min=-
∴t≥-
又由韦达定理可得a+b=-2t,ab=-1,b-a=2
若对于任意x∈[a,b],总存在x1,x2∈[a,b]使得f(x1)≤f(x)≤f(x2)恒成立,说明x1,x2分别是区间[a,b]f(x)的最小最大值点.
由(1)可得,f'(x)=
,注意h(x)=x2+2tx-1,不难发现函数f(x)在区间[a,b]
f'(x)≥0,f(x)递增,则x1=a,x2=b
则g(t)=f(x2)-f(x1)=f(b)-f(a)=
-
=
∵a+b=-2t,ab=-1,b-a=2
∴g(t)=
∵g(t)=
∴t=±2
| mx+t |
| x2+1 |
∴f′(x)=
| -mx2-2tx+m |
| (x2+1)2 |
∵函数f(x)=
| mx+t |
| x2+1 |
∴f′(0)=1
∴m=1
(2)由(1)知f(x)=
| x+t |
| x2+1 |
∵对于任意x∈[-1,2],总存在t,使得不等式f(x)≤2t成立
∴对于任意x∈[-1,2],总存在t,使得不等式t≥
| x |
| 2x2+1 |
| x |
| 2x2+1 |
令s(x)=
| x |
| 2x2+1 |
| -2x2+1 |
| (2x2+1)2 |
∴当s′(x)≥0时-
| ||
| 2 |
| ||
| 2 |
当s′(x)≤0时x≤-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴s(x)在[-1,-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∵s(-
| ||
| 2 |
| ||
| 4 |
| 2 |
| 9 |
∴s(x)min=-
| ||
| 4 |
∴t≥-
| ||
| 4 |
又由韦达定理可得a+b=-2t,ab=-1,b-a=2
| t2+1 |
若对于任意x∈[a,b],总存在x1,x2∈[a,b]使得f(x1)≤f(x)≤f(x2)恒成立,说明x1,x2分别是区间[a,b]f(x)的最小最大值点.
由(1)可得,f'(x)=
| -x2-2tx+1 |
| (x2+1)2 |
f'(x)≥0,f(x)递增,则x1=a,x2=b
则g(t)=f(x2)-f(x1)=f(b)-f(a)=
| b+t |
| b2+1 |
| a+t |
| a2+1 |
| ab(a-b)+(b-a)+t(a+b)(a-b) |
| (ab)2+(a+b)2-2ab+1 |
∵a+b=-2t,ab=-1,b-a=2
| t2+1 |
∴g(t)=
| t2+1 |
∵g(t)=
| 5 |
∴t=±2
点评:本题主要考查了导数求函数的几何意义,以及利用导数求函数的最大最小值问题,属常考题,较难.解题的关键是理解导数的几何意义即为函数在某点处切线的斜率以及根据方程x2+2tx-1=0的两个实数根为a,b(a<b)得出x2+2tx-1≤0在区间[a,b]恒成立即f'(x)≥0进而求出了最大最小值点!

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
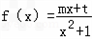 ,f(x)的图象在点M(0,f(0))处的切线的斜率为1.
,f(x)的图象在点M(0,f(0))处的切线的斜率为1. 时,求实数t的值.
时,求实数t的值.