题目内容
已知函数f(x)=x3-3tx+m(x∈R,m和t为实数)是奇函数.(Ⅰ)求实数m的值和函数f(x)的图像与横轴的交点坐标;
(Ⅱ)设g(x)=|f(x)|且x∈[-1,1],求g(x)的最大值F(t).
解:(1)依题意,m=0,
∴f(x)=x3-3tx. 令x3-3tx=0,
(1)当t=0时,x=0.
∴函数f(x)的图像与横轴的交点坐标为(0,0).
(2)当t>0时,x(x-3t)=0. ∴x=0,或x2=3t,
∴x=0,或x=![]() ,或x=
,或x=![]() ,
,
∴函数f(x)的图像与横轴的交点坐标为(0,0),或(![]() t,0),或(
t,0),或(![]() ,0).
,0).
(3)当t<0时,x(x-3t)=0. ∴x=0,或x2=3t(舍去).
∴函数f(x)的图像与横轴的交点坐标为(0,0).
(Ⅱ)g(x)=|f(x)|=|x3-3tx|,x∈[-1,1];
(1)当t=0时,g(x)=|x3|,x∈[-1,1];
F(t)=g(1)=g(-1)=1.
(2)当t<0时,F(t)=|f(l)=|1-3t|=1-3t.
(3)当t≥1时,F (t)=|f(1)=|1-3t|=3t-1.
(4)当0<t<1时,
x | 0 | (0, |
| ( | 1 |
f′(x) |
| - | 0 | + |
|
f(x) | 0 |
| 极小值-2t |
| 1-3t |
由g(x)的性质可知,
当![]() ≤t<1时,g(x)的最大值F(t)=-f(
≤t<1时,g(x)的最大值F(t)=-f(![]() )=2t
)=2t![]() .
.
当0<t<![]() 时,g(x)的最大值F(t)=f(1)=1-3t.
时,g(x)的最大值F(t)=f(1)=1-3t.
综上所述:F(t)=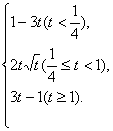

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目