题目内容
已知x，y满足x=
，则
的取值范围是（ ）
| 3-(y-2)2 |
| y+1 | ||
x+
|
分析：由已知中x，y满足x=
，可得（x，y）点落在半圆x2+（y-2）2=3，（x≥0），分析
的几何意义，数形结合可得答案．
| 3-(y-2)2 |
| y+1 | ||
x+
|
解答：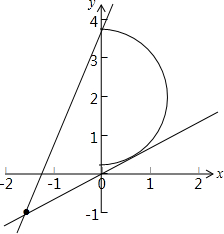
解：∵x，y满足x=
，
故（x，y）点落在半圆x2+（y-2）2=3，（x≥0）
表示半圆上动点（x，y）与（-
，-1）点连线的斜率，
如图所示：
由图可知当直线与半圆相切时，
=
当当直线与半圆相交于（0，2+
）时，
=
+1
故
的取值范围是[
，
+1]
故选D
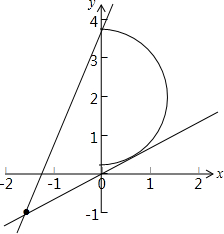解：∵x，y满足x=| 3-(y-2)2 |
故（x，y）点落在半圆x2+（y-2）2=3，（x≥0）
| y+1 | ||
x+
|
| 3 |
如图所示：
由图可知当直线与半圆相切时，
| y+1 | ||
x+
|
| ||
| 3 |
当当直线与半圆相交于（0，2+
| 3 |
| y+1 | ||
x+
|
| 3 |
故
| y+1 | ||
x+
|
| ||
| 3 |
| 3 |
故选D
点评：本题考查的知识点是直线与圆的位置关系，直线的斜率，其中分析出（x，y）点落在半圆x2+（y-2）2=3，（x≥0）上，及
的几何意义，是解答的关键．
| y+1 | ||
x+
|
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目