题目内容
已知x,y满足约束条件:2x-y≥0,x+y-2≥0,6x+3y≤18,且z=ax+y取得最大值的最优解恰为(| 3 | 2 |
分析:由题意应先有x,y满足约束条件:2x-y≥0,x+y-2≥0,6x+3y≤18,画出可行域,在利用目标函数z=ax+y的特点始终点(0,z),而直线的斜率在变化着,利用目标函的几何含义及图形即可求解.
解答:解:由x,y满足约束条件:2x-y≥0,x+y-2≥0,6x+3y≤18,画出如下图的线性可行域:
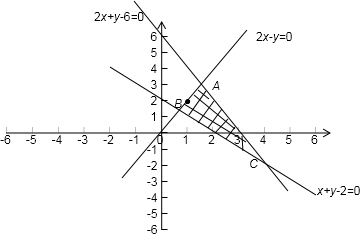
并有不等式组表示的为平面内的可行域的判断方法知道:该不等式表示的应为如上图的△ABC内部及其边界区域,
又由于目标函数为:z=ax+y?y=-ax+z,由该式子斜率为-a,并且随着a的值的变化而变化,又因为z=ax+y取得最大值的最优解恰为(
,3),所以可知当目标函数代表的直线介于直线2x-y=0与2x+y-6=0之间时才使得z=ax+y取得最大值的最优解恰为(
,3),
故-2<-a<2
即:-2<a<2,.
故答案为:-2<a<2

并有不等式组表示的为平面内的可行域的判断方法知道:该不等式表示的应为如上图的△ABC内部及其边界区域,
又由于目标函数为:z=ax+y?y=-ax+z,由该式子斜率为-a,并且随着a的值的变化而变化,又因为z=ax+y取得最大值的最优解恰为(
| 3 |
| 2 |
| 3 |
| 2 |
故-2<-a<2
即:-2<a<2,.
故答案为:-2<a<2
点评:此题考查了线性规划的知识,直线的方程及数形结合及等价转化的思想.

练习册系列答案
相关题目
 ,且
,且 ,若变量x,y满足约束条
,若变量x,y满足约束条 ,则z的最大值为
,则z的最大值为
 则z=2x-3y的最大值 .
则z=2x-3y的最大值 . 的最小值是
的最小值是