题目内容
设函数是定义在R上的增函数，且f(x)≠0，对任意x1，x2∈R，都有f(x1＋x2)＝f(x1)·f(x2)．
(1)求证：f(x)>0；
(2)求证：f(x1－x2)＝
；
(3)若f(1)＝2，解不等式f(3x)>4f(x)．
解：(1)证明：令x1＝x2＝
，
则f(t)＝f()·f()＝[f()]2.
∵f()≠0，∴f(t)>0，即f(x)>0.
(2)证明：∵f(x1)＝f(x1－x2＋x2)
＝f(x1－x2)·f(x2)．
∵f(x)≠0，∴f(x1－x2)＝.
(3)∵f(1)＝2，∴2f(x)＝f(1)·f(x)＝f(1＋x)，4f(x)＝2·2f(x)＝f(1)·f(x＋1)＝f(x＋2)，
则f(3x)>4f(x)即f(3x)>f(2＋x)．
∵f(x)是定义在R上的增函数．
∴3x>2＋x，∴x>1.
故不等式f(3x)>4f(x)的解集为(1，＋∞)．
练习册系列答案
相关题目
是定义在R上的奇函数，对任意实数
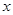有
成立．
是周期函数，并指出其周期；
，求
的值；
，且
是偶函数，求实数
的值．
是定义在R上的函数，其中
的导函数为
，满足
对于
恒成立，则（
）
B.
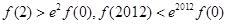
D.
是定义在R上的奇函数，且当x
0时，
是等差数列，且a3<0，则
的值为： 
是定义在R上的偶函数，且对任意的
恒有
，
时，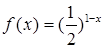
，则其中所有正确命题的序号是_____________.
上是减函数，在
上是增函数；
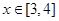时，
. 
是定义在R上的奇函数，若
， 
的取值范围是( )
B．
D．