题目内容
设函数 是定义在R上的偶函数,且对任意的
是定义在R上的偶函数,且对任意的 恒有
恒有 ,
,
已知当 时,
时,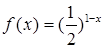 ,则其中所有正确命题的序号是_____________.
,则其中所有正确命题的序号是_____________.
① 2是函数 的周期; ② 函数
的周期; ② 函数 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
③ 函数 的最大值是1,最小值是0; ④ 当
的最大值是1,最小值是0; ④ 当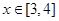 时,
时, .
.
【答案】
①②④
【解析】∵对任意的x∈R恒有f(x+1)=f(x-1),
∴f(x+2)=f(x)则f(x)的周期为2,故①正确;
∵函数f(x)是定义在R上的偶函数,当x∈[0,1]时,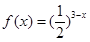
∴函数f(x)在(0,1)上是增函数,函数f(x)在(1,2)上是减函数,在(2,3)上是增函数,故②正确;
∴函数f(x)的最大值是f(1)=1,最小值为 ,故③不正确;
,故③不正确;
设x∈[3,4],则4-x∈[0,1], ,故④正确;
,故④正确;
故答案为:①②④

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 是定义在R上的奇函数,对任意实数
是定义在R上的奇函数,对任意实数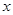 有
有 成立.
成立. 是周期函数,并指出其周期;
是周期函数,并指出其周期; ,求
,求 的值;
的值; ,且
,且 是偶函数,求实数
是偶函数,求实数 的值.
的值. 是定义在R上的函数,其中
是定义在R上的函数,其中 的导函数为
的导函数为 ,满足
,满足 对于
对于 恒成立,则(
)
恒成立,则(
) B.
B.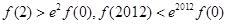
 D.
D.
 是定义在R上的奇函数,且当x
是定义在R上的奇函数,且当x 0时,
0时, 是等差数列,且a3<0,则
是等差数列,且a3<0,则 的值为:
的值为:  是定义在R上的奇函数,若
是定义在R上的奇函数,若 ,
,  的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.