题目内容
(1)解关于x的不等式:(a2+a-1)x>a2(1+x)+a-2(a∈R);(2)如果x=a2-4在上述不等式的解集中,求实数a的取值范围.
解:(1)(a2+a-1)x>a2(1+x)+a-2,
(a2+a-1)x-a2x>a2+a-2,
(a-1)x>a2+a-2,
(a-1)x>(a-1)(a+2),
当a>1时,解集为{x|x>a+2};
当a=1时,解集为∅;
当a<1时,解集为{x|x<a+2};
(2)解法一:由题意, 或
或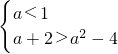 ,
,
分别化为: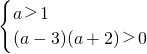 或
或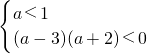 ,
,
解得:a>3或-2<a<1,
则实数a的取值范围为(-2,1)∪(3,+∞);
解法二:将x=a2-4代入原不等式,
并整理得:(a+2)(a-1)(a-3)>0,
根据题意画出图形,如图所示:
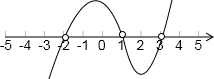
根据图形得:实数a的取值范围为(-2,1)∪(3,+∞).
分析:(1)把原不等式右边的未知项移项到左边进行合并,同时右边的式子分解因式,然后根据a-1大于0,a-1等于0及a-1小于0三种情况,根据不等式的基本性质把x的系数化为1,分别求出原不等式相应的解集即可;
(2)解法一:分两种情况:a大于1时,根据相应的解集列出关于a的不等式组;同理a小于1时列出相应的不等式组,求出两不等式组解集的并集即可得到a的范围;
解法二:把x=a2-4代入原不等式中化简,得到关于a的不等式,画出相应的图形,根据图形即可得到满足题意的a的取值范围.
点评:此题考查了其他不等式的解法,利用了分类讨论及数形结合的思想,第二小题有两种解法:一种是利用转化的思想,讨论a大于1和a小于1,根据第一问求出的解集列出相应的不等式组;另一种是直接把x的值代入原不等式,借助图形来求解.
(a2+a-1)x-a2x>a2+a-2,
(a-1)x>a2+a-2,
(a-1)x>(a-1)(a+2),
当a>1时,解集为{x|x>a+2};
当a=1时,解集为∅;
当a<1时,解集为{x|x<a+2};
(2)解法一:由题意,
 或
或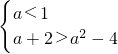 ,
,分别化为:
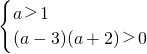 或
或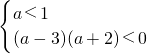 ,
,解得:a>3或-2<a<1,
则实数a的取值范围为(-2,1)∪(3,+∞);
解法二:将x=a2-4代入原不等式,
并整理得:(a+2)(a-1)(a-3)>0,
根据题意画出图形,如图所示:
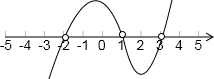
根据图形得:实数a的取值范围为(-2,1)∪(3,+∞).
分析:(1)把原不等式右边的未知项移项到左边进行合并,同时右边的式子分解因式,然后根据a-1大于0,a-1等于0及a-1小于0三种情况,根据不等式的基本性质把x的系数化为1,分别求出原不等式相应的解集即可;
(2)解法一:分两种情况:a大于1时,根据相应的解集列出关于a的不等式组;同理a小于1时列出相应的不等式组,求出两不等式组解集的并集即可得到a的范围;
解法二:把x=a2-4代入原不等式中化简,得到关于a的不等式,画出相应的图形,根据图形即可得到满足题意的a的取值范围.
点评:此题考查了其他不等式的解法,利用了分类讨论及数形结合的思想,第二小题有两种解法:一种是利用转化的思想,讨论a大于1和a小于1,根据第一问求出的解集列出相应的不等式组;另一种是直接把x的值代入原不等式,借助图形来求解.

练习册系列答案
相关题目
 已知不等式x2-2x-3<0解集为A,不等式x2+x-6<0的解集为B,
已知不等式x2-2x-3<0解集为A,不等式x2+x-6<0的解集为B,