题目内容
 已知不等式x2-2x-3<0解集为A,不等式x2+x-6<0的解集为B,
已知不等式x2-2x-3<0解集为A,不等式x2+x-6<0的解集为B,(1)求A∩B;
(2)若关于x的不等式x2+ax+b<0的解集为C,其A∩B⊆C,试写出实数a,b应满足的不等关系,并在给定坐标系中画出该不等关系所表示的平面区域.
分析:(1)解二次不等式求出A,B,然后直接求A∩B;
(2)关于x的不等式x2+ax+b<0的解集为C,其A∩B⊆C,推出二次函数满足的不等式组,即可写出实数a,b应满足的不等关系,直接在给定坐标系中画出该不等关系所表示的平面区域的应用部分.
(2)关于x的不等式x2+ax+b<0的解集为C,其A∩B⊆C,推出二次函数满足的不等式组,即可写出实数a,b应满足的不等关系,直接在给定坐标系中画出该不等关系所表示的平面区域的应用部分.
解答:解:(1)不等式x2-2x-3<0解集为A,不等式x2+x-6<0的解集为B,
∴A={x|-1<x<3},
B={x|-3<x<2},
∴A∩B={x|-1<x<3}∩{x|-3<x<2}
={X|-1<x<2};
(2)记f(x)=x2+ax+b,由已知
,
⇒
,
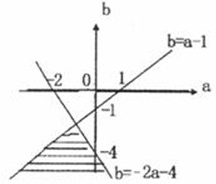
所表示的平面区域的部分如图中阴影部分.
∴A={x|-1<x<3},
B={x|-3<x<2},
∴A∩B={x|-1<x<3}∩{x|-3<x<2}
={X|-1<x<2};
(2)记f(x)=x2+ax+b,由已知
|
⇒
|
所表示的平面区域的部分如图中阴影部分.

点评:本题是基础题,考查二次不等式的解法,集合的交集的求法,线性规划的应用,考查计算能力,作图能力.

练习册系列答案
相关题目