题目内容

【题目】已知抛物线，直线过抛物线焦点，且与抛物线交于， 两点，以线段为直径的圆与抛物线准线的位置关系是（ ）

A. 相离 B. 相交 C. 相切 D. 不确定

【答案】C

【解析】取AB的中点M,分别过A,B,M作准线的垂线AP,BQ,MN,垂足分别为P,Q,N,如图所示,由抛物线的定义可知, ,在直角梯形APQB中, ,故圆心M到准线的距离等于半径,所以以AB为直径的圆与抛物线的准线相切,故选C.

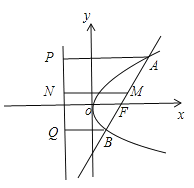
点睛:本题考查直线与圆的位置关系以及抛物线的定义的应用,属于中档题. 以线段为直径的圆的圆心为AB中点M,圆心到抛物线准线的距离为MN,由图可知MN为梯形APQB的中位线,即,再根据椭圆的定义可得,圆心M到准线的距离等于半径,故直线与圆相切.

练习册系列答案
相关题目

【题目】如图是一几何体的平面展开图，其中ABCD为正方形，E，F分别为PA，PD的中点，

在此几何体中，给出下面四个结论：

①直线BE与直线CF异面； ②直线BE与直线AF异面；

③直线EF∥平面PBC； ④平面BCE⊥平面PAD.

其中正确的有(　　)

A. 1个 B. 2个 C. 3个 D. 4个

【题目】如图，三棱柱中，底面为正三角形， 底面，且， 是的中点.

（1）求证： 平面；

（2）求证：平面平面；

（3）在侧棱上是否存在一点，使得三棱锥的体积是？若存在，求出的长；若不存在，说明理由.

【题目】已知圆的圆心在直线上，且与另一条直线相切于点.

（1）求圆的标准方程；

（2）已知，点在圆上运动，求线段的中点的轨迹方程.

【题目】如图，在三棱柱中， 底面， ， ， ， 是棱上一点．

（I）求证： ．

（II）若， 分别是， 的中点，求证： 平面．

（III）若二面角的大小为，求线段的长．

【题目】已知函数y=f(x)，f(0)=-2，且对，yR，都有f(x+y)-f(y)=(x+2y+1)x.

（1）求f(x)的表达式；

（2）已知关于x的不等式f(x)-ax+a+1的解集为A，若A[2,3]，求实数a的取值范围；

（3）已知数列{}中， ， ，记，且数列{的前n项和为，

求证： .

【题目】已知过点A(0，1)且斜率为k的直线l与圆C：(x－2)2＋(y－3)2＝1交于M，N两点．

(1)求k的取值范围；

(2)若＝12，其中O为坐标原点，求|MN|.

【题目】已知⊙H被直线x-y-1=0,x+y-3=0分成面积相等的四个部分,且截x轴所得线段的长为2。

(I)求⊙H的方程;

(Ⅱ)若存在过点P(0,b)的直线与⊙H相交于M，N两点,且点M恰好是线段PN的中点,求实数b的取值范围

【题目】已知， 是抛物线上两点，且与两点横坐标之和为3.

(1)求直线的斜率；

(2)若直线，直线与抛物线相切于点，且，求方程.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网