题目内容
12．已知直线2x+y-c=0与圆x2+y2=R2交于A，B两点，则与$\overrightarrow{OA}+\overrightarrow{OB}$（O为坐标原点）共线的向量是（ ）| A． | （2，-1） | B． | （-2，-4） | C． | （4，2） | D． | （-1，2） |
分析 本题可通过设A，B两点坐标，联立方程求出向量坐标，再利用共线向量坐标成比例得出．
解答 解：设A（x1，y1），B（x2，y2），则$\overrightarrow{OA}+\overrightarrow{OB}$=（x1+x2，y1+y2）
由直线方程得y=-2x+c，代入圆的方程得：5x2-4xc+c2-R2=0
则x1，x2为方程两根，x1+x2=$\frac{4c}{5}$，
代入y=-2x+c得y1+y2=-$\frac{8c}{5}$+2c=$\frac{2}{5}c$
则$\overrightarrow{OA}+\overrightarrow{OB}$=（$\frac{4c}{5}，\frac{2c}{5}$）
设所求向量为（x，y），则$\frac{4cy}{5}=\frac{2cx}{5}$，所以2y=x；
故选C．
点评 本题考查向量共线的充要条件．
练习册系列答案
相关题目
2．已知函数f（x）=$\sqrt{3}$sinωx+cosωx（ω＞0）的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列，把函数f（x）的图象沿x轴向左平移$\frac{π}{6}$个单位，得到函数g（x）的图象．关于函数g（x），下列说法正确的是（ ）
| A． | 在[$\frac{π}{4}$，$\frac{π}{2}$]上是增函数 | |
| B． | 其图象关于直线x=-$\frac{π}{4}$对称 | |
| C． | 函数g（x）是奇函数 | |
| D． | 当x∈[$\frac{π}{6}$，$\frac{2}{3}$π]时，函数g（x）的值域是[-2，1] |
7．定义在R上的函数f（x）对任意x1、x2（x1≠x2）都有$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＜0，且函数y=f（x-1）的图象关于（1，0）成中心对称，若s，t满足不等式f（s2-2s）≤-f（2t-t2），则当1≤s≤4时，$\frac{t-2s}{s+t}$的取值范围是（ ）
| A． | [-3，-$\frac{1}{2}$） | B． | [-3，-$\frac{1}{2}$] | C． | [-5，-$\frac{1}{2}$） | D． | [-5，-$\frac{1}{2}$] |
4．已知点P（-1，m），A（1，0）且$\overrightarrow{PQ}$=2$\overrightarrow{QA}$，若点Q在抛物线y2=4x上，则m=（ ）
| A． | ±2 | B． | ±$\sqrt{3}$ | C． | ±$\frac{2\sqrt{3}}{3}$ | D． | ±3 |
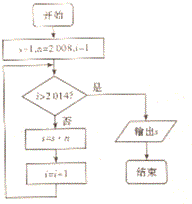如图所示的流程图，根据最后输出的变量s的值，得s的末位数值是4．