题目内容
(本小题满分12分)
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90O,∠EAC=600,AB=AC=AE.
(1)在直线BC上是否存在一点P,使得DP∥平面EAB?请证明你的结论;
(2)求平面EBD与平面ABC所成的锐二面角 的大小。
的大小。

【答案】
证明如下:
取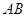 的中点
的中点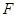 连结
连结 ,则
,则
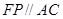 ,
, ,
,
取 的中点
的中点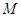 ,连结
,连结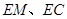 ,
,
∵ 且
且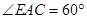 ,
,
∴△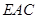 是正三角形,∴
是正三角形,∴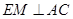 .
.
∴四边形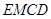 为矩形,∴
为矩形,∴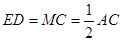 .又∵
.又∵ ,
,
∴ 且
且 ,四边形
,四边形 是平行四边形.
是平行四边形.
∴ ,而
,而 平面
平面 ,
, 平面
平面 ,∴
,∴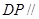 平面
平面 6分
6分
(或可以证明面面平行)
(2)(法1)过 作
作 的平行线
的平行线 ,过
,过 作
作 的垂线交
的垂线交 于
于 ,连结
,连结 ,
,

∵ ,∴
,∴ ,
, 是平面
是平面 与平面
与平面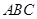 所成二面角的棱 8分
所成二面角的棱 8分
∵平面 平面
平面 ,
,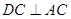 ,∴
,∴ 平面
平面 ,
,
又∵ 平面
平面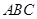 ,
, ∴
∴ 平面
平面 ,∴
,∴ ,
,
∴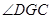 是所求二面角的平面角. 10分
是所求二面角的平面角. 10分
设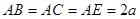 ,则
,则 ,
, ,
,
∴ ,
,
∴ .
.
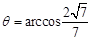 12分
12分
(法2)∵ ,平面
,平面 平面
平面 ,
,
∴以点 为原点,直线
为原点,直线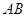 为
为 轴,直线
轴,直线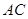 为
为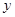 轴,
轴,
建立空间直角坐标系 ,则
,则 轴在平面
轴在平面 内(如图).
内(如图).

设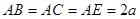 ,由已知,得
,由已知,得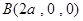 ,
,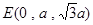 ,
,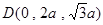 .
.
∴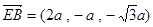 ,
, ,…………………8分
,…………………8分
设平面 的法向量为
的法向量为 ,
,
则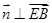 且
且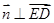 ,
,
∴ ∴
∴ 解之得
解之得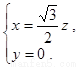
取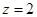 ,得平面
,得平面 的一个法向量为
的一个法向量为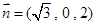 .
.
又∵平面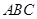 的一个法向量为
的一个法向量为 .
.
 .
.
 12分
12分
【解析】略

练习册系列答案
相关题目