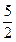题目内容
设函数f(x)=x2+|x-2|-1,x∈R.
(1)判断函数f(x)的奇偶性;
(2)求函数f(x)的最小值
(1)判断函数f(x)的奇偶性;
(2)求函数f(x)的最小值
(1)f(x)=
∵f(0)=1≠0,∴f(x)不是R上的奇函数.
∵f(1)=1,f(-1)=3,f(1)≠f(-1),
∴f(x)不是偶函数.故f(x)是非奇非偶的函数.
(2)当x≥2时,f(x)=x2+x-3,此时f(x)min=f(2)=3.
当x<2时,f(x)=x2-x+1,此时f(x)min=f=.
所以,f(x)min=.
∵f(0)=1≠0,∴f(x)不是R上的奇函数.
∵f(1)=1,f(-1)=3,f(1)≠f(-1),
∴f(x)不是偶函数.故f(x)是非奇非偶的函数.
(2)当x≥2时,f(x)=x2+x-3,此时f(x)min=f(2)=3.
当x<2时,f(x)=x2-x+1,此时f(x)min=f=.
所以,f(x)min=.
略

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
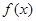 在区间
在区间 上单调递增,则满足
上单调递增,则满足 的x的取
的x的取


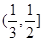
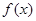 是R上的单调减函数且为奇函数,则
是R上的单调减函数且为奇函数,则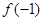 的值( )
的值( ) 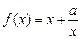 (
(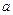 为常数)的图象过点
为常数)的图象过点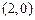 ,
,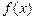 的奇偶性;
的奇偶性;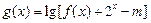 在区间
在区间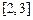 上
上 有意义,求实数
有意义,求实数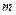 的取值范围;
的取值范围; 的方程
的方程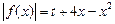
 (
(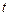 为常数)的正根的个数.
为常数)的正根的个数.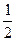 (a x+a -x), (a>0且a≠1)
(a x+a -x), (a>0且a≠1)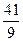 ), 求f(x)
), 求f(x)
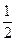 ,
, f(x+2)=f(x)+f(2),则f(5)=
f(x+2)=f(x)+f(2),则f(5)=