题目内容
当 时
时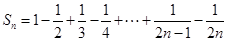 ,
,

(1)求
(2)猜想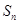 与
与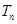 的关系,并用数学归纳法证明。
的关系,并用数学归纳法证明。
 时
时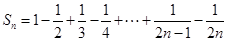 ,
,
(1)求

(2)猜想
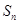 与
与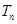 的关系,并用数学归纳法证明。
的关系,并用数学归纳法证明。(1)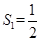 ,
,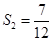 ,
,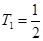 ,
,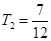
(2)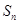 =
=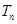 ,理由见解析
,理由见解析
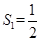 ,
,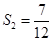 ,
,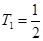 ,
,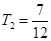
(2)
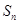 =
=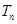 ,理由见解析
,理由见解析试题分析:解:(1)
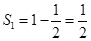 ,
,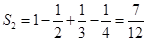
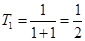 ,
,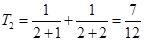
(2)猜想:
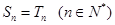 即:
即: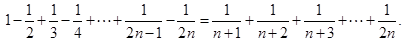 (n∈N*)
(n∈N*) 下面用数学归纳法证明
n=1时,已证S1=T1
假设n=k时,Sk=Tk(k≥1,k∈N*),即:
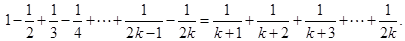
则
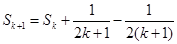
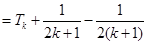
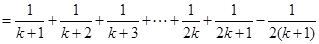
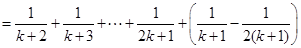
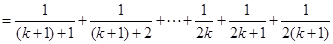
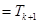
由①,②可知,对任意n∈N*,Sn=Tn都成立.
点评:本题用到的数学归纳法,在高中数学中常用来证明等式成立和数列通项公式成立。若要证明一个与自然数n有关的命题P(n),有如下步骤:
(1)证明当n取第一个值
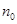 时命题成立。
时命题成立。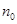 对于一般数列取值为0或1,但也有特殊情况;
对于一般数列取值为0或1,但也有特殊情况;(2)假设当n=k(k≥
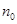 ,k为自然数)时命题成立,证明当n=k+1时命题也成立。
,k为自然数)时命题成立,证明当n=k+1时命题也成立。综合(1)(2),对一切自然数n(≥
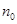 ),命题P(n)都成立。
),命题P(n)都成立。
练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目

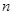 个小球,将它们任意分成两堆,求出这两堆小球球数的乘积,再将其中一堆小球任意分成两堆,求出这两堆小球球数的乘积,如此下去,每次都任选一堆,将这堆小球任意分成两堆,求出这两堆小球球数的乘积,直到不能再分为止,则所有乘积的和为 .
个小球,将它们任意分成两堆,求出这两堆小球球数的乘积,再将其中一堆小球任意分成两堆,求出这两堆小球球数的乘积,如此下去,每次都任选一堆,将这堆小球任意分成两堆,求出这两堆小球球数的乘积,直到不能再分为止,则所有乘积的和为 .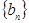 中,若
中,若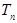 是数列
是数列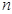 项积,则有
项积,则有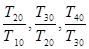 也成等比数列,且公比为
也成等比数列,且公比为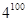 ;类比上述结论,相应的在公差为3的等差数列
;类比上述结论,相应的在公差为3的等差数列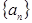 中,若
中,若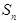 是
是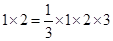 ,
,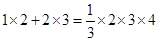 ,
,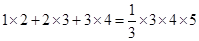 ,…, 照此规律,
,…, 照此规律,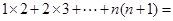 (
(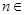 N
N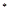 ).
).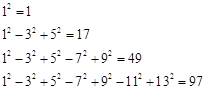
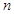 个等式________________________________________.
个等式________________________________________.