题目内容
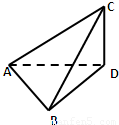
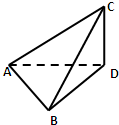 如图,CD是一座铁塔,线段AB和塔底D在同一水平地面上,在A,B两点测得塔顶C的仰角分别为60°和45°,又测得AB=24m,∠ADB=30°,则此铁塔的高度为
如图,CD是一座铁塔,线段AB和塔底D在同一水平地面上,在A,B两点测得塔顶C的仰角分别为60°和45°,又测得AB=24m,∠ADB=30°,则此铁塔的高度为24
| 3 |
24
m.| 3 |
分析:先确定AD,BD的长,再利用余弦定理,即可求得铁塔的高度.
解答:解:设铁塔的高度为hm,则
∵A,B两点测得塔顶C的仰角分别为60°和45°,
∴AD=CDtan(90°-60°)=
hm,BD=hm,
在△ABD中,AB=24m,∠ADB=30°,∴由余弦定理可得242=
h2+h2-2×
h×h×cos30°
∴h=24
m
故答案为:24
m.
∵A,B两点测得塔顶C的仰角分别为60°和45°,
∴AD=CDtan(90°-60°)=
| ||
| 3 |
在△ABD中,AB=24m,∠ADB=30°,∴由余弦定理可得242=
| 1 |
| 3 |
| ||
| 3 |
∴h=24
| 3 |
故答案为:24
| 3 |
点评:本题考查解三角形的实际应用,考查余弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
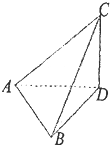 如图,CD是一座铁塔,线段AB和塔底D在同一水平地面上,在A,B两点测得塔顶C的仰角分别为60°和45°,又测得AB=24m∠ADB=30°,则此铁塔的高度为( )m.
如图,CD是一座铁塔,线段AB和塔底D在同一水平地面上,在A,B两点测得塔顶C的仰角分别为60°和45°,又测得AB=24m∠ADB=30°,则此铁塔的高度为( )m.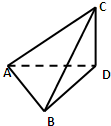 如图,CD是一座铁塔,线段AB和塔底D在同一水平地面上,在A,B两点测得塔顶C的仰角分别为30°和45°,又测得AB=12m,∠ADB=30°则此铁塔的高度为
如图,CD是一座铁塔,线段AB和塔底D在同一水平地面上,在A,B两点测得塔顶C的仰角分别为30°和45°,又测得AB=12m,∠ADB=30°则此铁塔的高度为