题目内容
设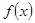 是定义在
是定义在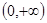 上的函数,且
上的函数,且 ,对任意
,对任意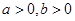 ,若经过点
,若经过点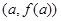 ,
,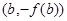 的直线与
的直线与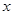 轴的交点为
轴的交点为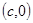 ,则称
,则称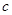 为
为 关于函数
关于函数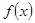 的平均数,记为
的平均数,记为 ,例如,当
,例如,当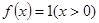 时,可得
时,可得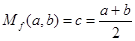 ,即
,即 为
为 的算术平均数.
的算术平均数.
当 时,
时, 为
为 的几何平均数;
的几何平均数;
当 时,
时, 为
为 的调和平均数
的调和平均数 ;
;
(以上两空各只需写出一个符合要求的函数即可)
(1)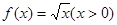 ;(2)
;(2)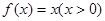 .
.
解析试题分析:设 ,则三点共线:
,则三点共线:
①依题意,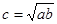 ,则
,则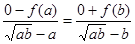 ,
, ,化简得
,化简得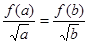 ,
,
故可以选择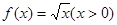 .
.
②依题意,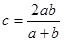 ,则
,则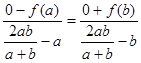 ,
, ,化简得
,化简得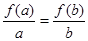 ,
,
故可以选择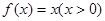 .
.
考点:两个数的几何平均数与调和平均数,难度中等.新定义型试题是高考的热点试题,考生错误往往有二,其一为不能正确理解题意,将新问题转化为所熟悉的数学问题;其二,不具备归纳、猜想、推理、传化等数学能力.但纵观湖北近四年高考试题,新定义型试题是必考试题,在专题复习中应加强训练.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
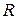 上的偶函数
上的偶函数 满足:
满足: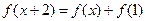 且在区间
且在区间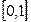 上
上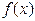 性质的表述:
性质的表述: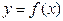 的图象关于直线
的图象关于直线 对称; ②函数
对称; ②函数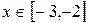 时,
时, ; ④函数
; ④函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个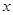 都成立,则称函数
都成立,则称函数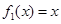 是否为 “(
是否为 “(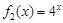 是“(
是“(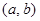 ;
; 是“
是“ 型函数”,对应的实数对
型函数”,对应的实数对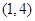 ,当
,当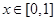 时,
时,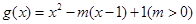 ,若当
,若当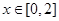 时,都有
时,都有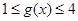 ,试求
,试求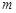 的取值范围.
的取值范围.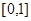 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件: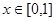 ,总有
,总有 ;
;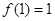 ;
; 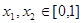 ,且
,且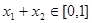 时,
时,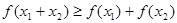 成立.
成立.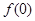 的值;
的值;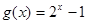 在区间
在区间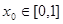 ,使得
,使得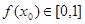 ,且
,且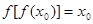 ,求证:
,求证: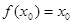 .
. .
. ,函数
,函数 在区间
在区间 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围;
的取值范围;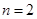 ,若对任意
,若对任意 恒成立,求
恒成立,求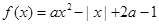 (
( 为实常数).
为实常数).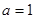 ,求函数
,求函数 的单调区间;
的单调区间;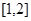 上的最小值为
上的最小值为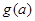 ,求
,求
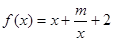 (
(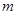 为实常数).
为实常数). 在区间
在区间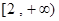 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数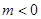 ,若不等式
,若不等式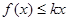 在
在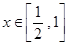 有解,求
有解,求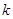 的取值范围.
的取值范围.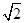 ),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.