题目内容
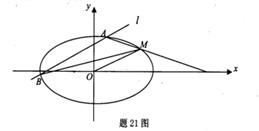
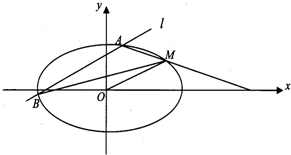
如图,已知离心率为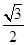 的椭圆
的椭圆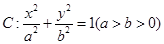 过点M(2,1),O为坐标原点,平行于OM的直线
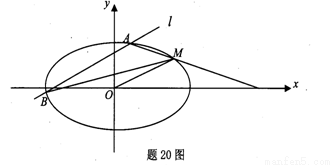
过点M(2,1),O为坐标原点,平行于OM的直线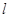 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。
(1)求椭圆C的方程。
(2)证明:直线MA、MB与x轴围成一个等腰三角形。
【答案】
解:(Ⅰ)设椭圆 的方程为:
的方程为: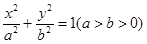 .
.
由题意得: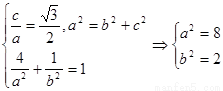
∴ 椭圆方程为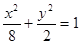 .……………5分
.……………5分
(Ⅱ)由直线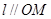 ,可设
,可设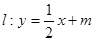 将式子代入椭圆
将式子代入椭圆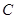 得:
得: 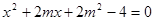
设 ,则
,则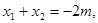
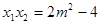 …
…
设直线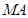 、
、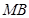 的斜率分别为
的斜率分别为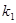 、
、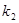 ,则
,则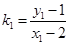
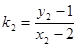 ……………8分
……………8分
下面只需证明: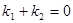 ,事实上,
,事实上,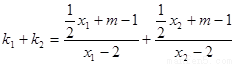
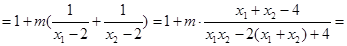
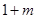
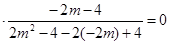
故直线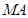 、
、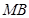 与
与 轴围成一个等腰三角形.……………12分
轴围成一个等腰三角形.……………12分
【解析】略

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 如图,已知离心率为
如图,已知离心率为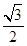 的椭圆
的椭圆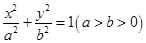 上的点到左焦点
上的点到左焦点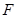 的最长距离为
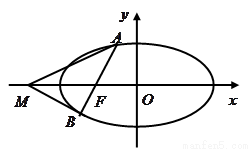
的最长距离为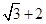 .
.
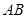 ,若点
,若点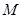 在
在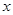 轴上,且使得
轴上,且使得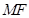 为
为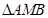 的一条内角平分线,则称点
的一条内角平分线,则称点 的椭圆
的椭圆 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。
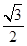 的椭圆
的椭圆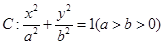 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线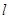 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。 面积的最大值;
面积的最大值;