题目内容
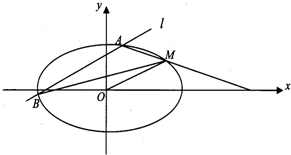 如图,已知离心率为
如图,已知离心率为
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的方程.
(2)证明:直线MA、MB与x轴围成一个等腰三角形.
分析:(Ⅰ)先由椭圆C:
+
=1(a>b>0)的离心率为
和椭圆过点M(2,1),列出方程组,再由方程组求出a,b,由此能求出椭圆方程.
(Ⅱ)由直线l∥OM,设l:y=
x+m,将式子代入椭圆C得:x2+2mx+2m2-4=0,设直线MA、MB的斜率分别为k1,k2,欲证明直线MA、MB与x轴围成一个等腰三角形.只需证明:k1+k2=0即可.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅱ)由直线l∥OM,设l:y=
| 1 |
| 2 |
解答:(Ⅰ)解:设椭圆C的方程为:
+
=1(a>b>0),
由题意得:
,
解得a2=8,b2=2,
∴椭圆方程为
+
=1.
(Ⅱ)证明:由直线l∥OM,设l:y=
x+m,
将式子代入椭圆C得:x2+2mx+2m2-4=0,
设A(x1,y1),B(x2,y2),则x1+x2=-2m,x1x2=2m2-4,
设直线MA、MB的斜率分别为k1,k2,
则k1=
,k2=
,
∵k1+k2=
+
=1+m•
=1+m•
=0,
故直线MA、MB与x轴围成一个等腰三角形.
| x2 |
| a2 |
| y2 |
| b2 |
由题意得:
|
解得a2=8,b2=2,
∴椭圆方程为
| x2 |
| 8 |
| y2 |
| 2 |
(Ⅱ)证明:由直线l∥OM,设l:y=
| 1 |
| 2 |
将式子代入椭圆C得:x2+2mx+2m2-4=0,
设A(x1,y1),B(x2,y2),则x1+x2=-2m,x1x2=2m2-4,
设直线MA、MB的斜率分别为k1,k2,
则k1=
| y1-1 |
| x1-2 |
| y2-1 |
| x2-2 |
∵k1+k2=
| ||
| x1-2 |
| ||
| x2-2 |
=1+m•
| x1+x2-4 |
| x1x2-2(x1+x2)+4 |
=1+m•
| -2m-4 |
| 2m2-4-2(-2m)+4 |
故直线MA、MB与x轴围成一个等腰三角形.
点评:本题考查椭圆方程的求法,考查三角形是等腰三角形的证明,解题时要认真审题,仔细解答,注意直线与椭圆的位置关系的灵活运用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图,已知双曲线E:
如图,已知双曲线E: 如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为
如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为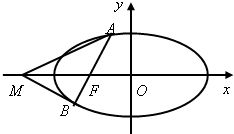 已知离心率为
已知离心率为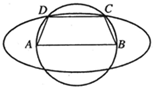 如图,已知AB=2c(常数c>0),以AB为直径的圆有一内接梯形ABCD,且AB∥CD,若椭圆以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,椭圆的离心率为
如图,已知AB=2c(常数c>0),以AB为直径的圆有一内接梯形ABCD,且AB∥CD,若椭圆以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,椭圆的离心率为