题目内容
已知离心率为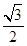 的椭圆
的椭圆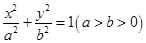 上的点到左焦点
上的点到左焦点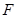 的最长距离为
的最长距离为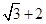 .
.
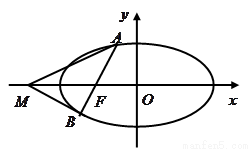
(Ⅰ)求椭圆的方程;
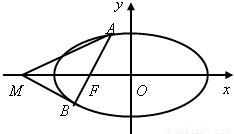
(Ⅱ)如图,过椭圆的左焦点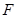 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦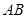 ,若点
,若点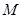 在
在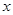 轴上,且使得
轴上,且使得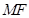 为
为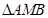 的一条内角平分线,则称点
的一条内角平分线,则称点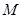 为该椭圆的“左特征点”,求椭圆的“左特征点”
为该椭圆的“左特征点”,求椭圆的“左特征点”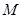 的坐标.
的坐标.
【答案】
(1)椭圆的方程为 ,其准线方程为
,其准线方程为 ;(2)
;(2) .
.
【解析】
试题分析:(1)由题意知: ,解得
,解得 ,
, ,
,
故椭圆的方程为 ,其准线方程为
,其准线方程为 4分
4分
(2)设 为椭圆
为椭圆 的左特征点,椭圆的左焦点为
的左特征点,椭圆的左焦点为 ,可设直线
,可设直线 的方程为:
的方程为: ,
,
联立方程组 ,消去
,消去 得
得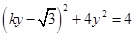 ,即
,即 ,
,
设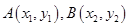 ,则
,则
∵ 被
被 轴平分,∴
轴平分,∴ ,即
,即 ,
,
 ,
,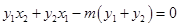
即 ,
,
∴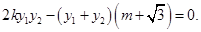 于是,
于是,
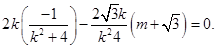
∵ ,∴
,∴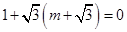 ,即
,即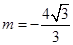 ,∴
,∴ .
.
考点:本题主要考查椭圆的标准方程,椭圆的几何性质,直线与椭圆的位置关系,三角形面积计算。
点评:中档题,不必太其椭圆的标准方程,主要运用了椭圆的几何性质,a,b,c,e的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)涉及新定义问题,注意理解其实质内容。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 的椭圆
的椭圆 上的点到
上的点到 的最长距离为
的最长距离为
 ,若点
,若点 在
在 轴上,且使得
轴上,且使得 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点
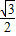 的椭圆
的椭圆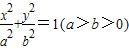 上的点到左焦点F的最长距离为
上的点到左焦点F的最长距离为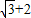 .
.
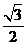 的椭圆
的椭圆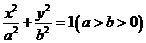 上的点到左焦点
上的点到左焦点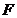 的最长距离为
的最长距离为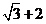 .
.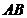 ,若点
,若点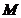 在
在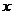 轴上,且使得
轴上,且使得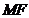 为
为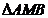 的一条内角平分线,则称点
的一条内角平分线,则称点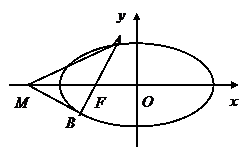
 的椭圆
的椭圆 上的点到左焦点
上的点到左焦点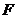 的最长距离为
的最长距离为
 ,若点
,若点 在
在 轴上,且使得
轴上,且使得 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点