题目内容
某商品每件成本为80元,当每件售价为100元时,每天可以售出100件.若售价降低10x%,售出商品的数量就增加16x%.
(1)试建立该商品一天的营业额y(元)关于x的函数关系式;
(2)若要求该商品一天的营业额至少为10260元,且又不能亏本,求x的取值范围.
(1)试建立该商品一天的营业额y(元)关于x的函数关系式;
(2)若要求该商品一天的营业额至少为10260元,且又不能亏本,求x的取值范围.
(1)所求函数关系式为y=100(1-0.1x)•100(1+0.16x)(x>0)…(3分)
又售价不能低于成本价,所以100(1-
)-80≥0,解得0≤x≤2.
∴y=100(1-0.1x)•100(1+0.16x),定义域为[0,2].
(不写定义域不扣分)
(2)依题意建立不等式组:
…(6分)
解(1)得:
≤x≤
…(8分)
解(2)得:x≤2…(9分)
综上所述,
≤x≤2,即x的取值范围是[
,2].…(10分)
说明:无不等式(2)共扣(2分).
又售价不能低于成本价,所以100(1-
| x |
| 10 |
∴y=100(1-0.1x)•100(1+0.16x),定义域为[0,2].
(不写定义域不扣分)
(2)依题意建立不等式组:
|
解(1)得:
| 1 |
| 2 |
| 13 |
| 4 |
解(2)得:x≤2…(9分)
综上所述,
| 1 |
| 2 |
| 1 |
| 2 |
说明:无不等式(2)共扣(2分).

练习册系列答案
相关题目
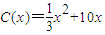 (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时, (万元).现已知此商品每件售价为500元,且该厂年内生产此商品能全部销售完.
(万元).现已知此商品每件售价为500元,且该厂年内生产此商品能全部销售完.