题目内容
(本小题满分12分)
已知椭圆 的离心率为
的离心率为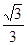 ,过右焦点F的直线
,过右焦点F的直线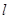 与C相交于A、B两点,当直线
与C相交于A、B两点,当直线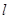 的斜率为1时,坐标原点O到
的斜率为1时,坐标原点O到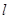 的距离为
的距离为 。
。
(1)求 的值;
的值;
(2)椭圆C上是否存在点P,使得当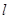 绕F转到某一位置时,有
绕F转到某一位置时,有 成立?若存在,求出所有的点P的坐标与
成立?若存在,求出所有的点P的坐标与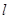 的方程;若不存在,说明理由
的方程;若不存在,说明理由
【答案】
(1)设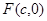 ,当
,当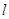 的斜率为1时,其方程为
的斜率为1时,其方程为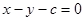 ,
,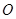 到
到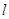 的距离为
的距离为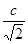 。故
。故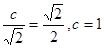 。由
。由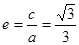 ,得
,得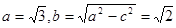
(2)若椭圆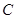 上存在点
上存在点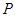 ,使得当
,使得当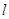 绕
绕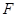 转到某一位置时,有
转到某一位置时,有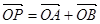 成立,
成立,
由(1)知椭圆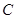 的方程为
的方程为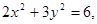 设
设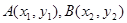
1)当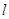 垂直于
垂直于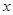 轴时,由
轴时,由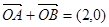 知,椭圆
知,椭圆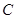 上不存在点
上不存在点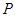 ,
,
2)使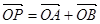 成立
成立
3)当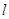 不垂直于
不垂直于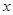 轴时,设
轴时,设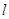 的方程为
的方程为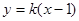 ,代入
,代入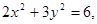 得
得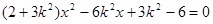 ,
,
4)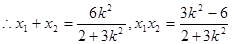 。由
。由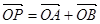 知,
知,
5)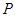 点的坐标为
点的坐标为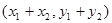 ,
,
6)满足椭圆C的方程,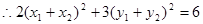 ,
,
又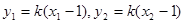 代入得
代入得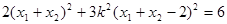 ,
,
解得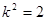
当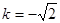 时,
时,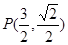 ,直线
,直线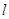 的方程为
的方程为
当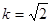 时,
时,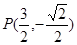 ,直线
,直线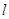 的方程为
的方程为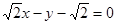
综上,椭圆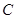 上存在点
上存在点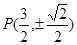 ,使
,使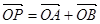 成立,
成立,
此时直线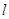 的方程为
的方程为
【解析】略

练习册系列答案
相关题目