题目内容
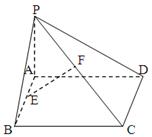
如图所示,已知AC ⊥平面CDE, BD ∥AC , 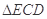 为等边三角形,F为ED边上的中点,且
为等边三角形,F为ED边上的中点,且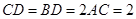 ,
,
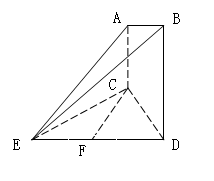
(Ⅰ)求证:CF∥面ABE;
(Ⅱ)求证:面ABE ⊥平面BDE;
(Ⅲ)求该几何体ABECD的体积。
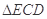 为等边三角形,F为ED边上的中点,且
为等边三角形,F为ED边上的中点,且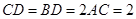 ,
,
(Ⅰ)求证:CF∥面ABE;
(Ⅱ)求证:面ABE ⊥平面BDE;
(Ⅲ)求该几何体ABECD的体积。
(1)证明:取BE的中点G,由中位线定理CF∥AG得到CF∥面ABE;
(2)由△ECD为等边三角形得到CF⊥ED,又由CF⊥BD得CF⊥面BDE,所以AG⊥面BDE,从而面ABE ⊥平面BDE ;
(3)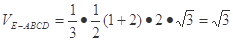 。
。
(2)由△ECD为等边三角形得到CF⊥ED,又由CF⊥BD得CF⊥面BDE,所以AG⊥面BDE,从而面ABE ⊥平面BDE ;
(3)
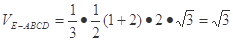 。
。试题分析:(1)证明:取BE的中点G,连FG∥
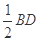 ,AC∥
,AC∥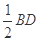 ,故CF∥AG
,故CF∥AG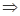 CF∥面ABE (4分)
CF∥面ABE (4分)(2)证明:△ECD为等边三角形
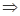 CF⊥ED又CF⊥BD
CF⊥ED又CF⊥BD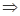 CF⊥面BDE
CF⊥面BDECF∥AG
故AG⊥面BDE
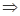 面ABE ⊥平面BDE (8分)
面ABE ⊥平面BDE (8分)(3)几何体ABECD是四棱锥E-ABCD,EH⊥CD
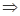 EH⊥面ABCD
EH⊥面ABCD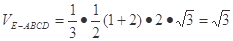 (12分)
(12分)点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,(1)小题,将立体问题转化成平面问题,这也是解决立体几何问题的一个基本思路。

练习册系列答案
相关题目
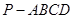 中,底面
中,底面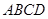 是矩形,
是矩形,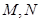 分别为
分别为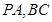 的中点,
的中点,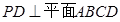 ,且
,且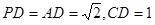
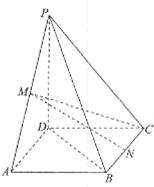
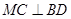 ;
;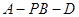 的余弦值。
的余弦值。 β且α⊥β,则l⊥α
β且α⊥β,则l⊥α β=m,且l∥m, 则l∥α
β=m,且l∥m, 则l∥α 的正方体
的正方体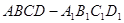 中,
中,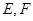 分别为
分别为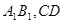 的中点.
的中点.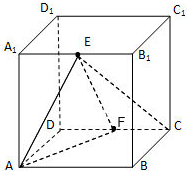
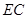 与平面
与平面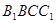 所 成 角的大小;
所 成 角的大小;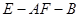 的大小.
的大小.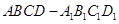 中,设
中,设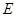 是棱
是棱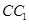 的中点.
的中点.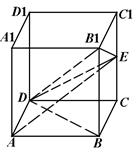
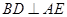 ;
;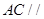 平面
平面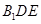 ;
;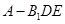 的体积.
的体积.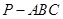 中,
中,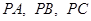 两两垂直,且
两两垂直,且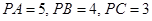 .设点
.设点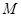 为底面
为底面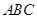 内一点,定义
内一点,定义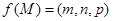 ,其中
,其中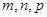 分别为三棱锥
分别为三棱锥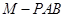 、
、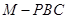 、
、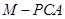 的体积.若
的体积.若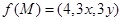 ,且
,且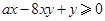 恒成立,则正实数
恒成立,则正实数 的取值范围是___________.
的取值范围是___________.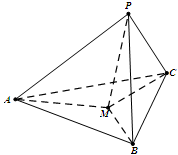
 个
个 个
个 个
个