题目内容
用定义证明：函数
在x∈[2，+∞）上是增函数．
证明：设x1，x2∈∈[2，+∞）且x1＜x2
f（x1）-f（x2）=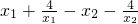
=
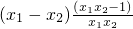＜0
∴函数在x∈[2，+∞）上是增函数
分析：要求用定义证明，则先在给定的区间上任取两个变量，且界大小，再作差变形看符号，若自变量与相应函数值变化一致，则为增函数，若自变量变化与相应函数值变化相反时，则为减函数．
点评：本题主要考查用单调性定义如何来证明函数单调性的，要注意几点：一是自变量的任意性，二是来自相应的区间，三是变形要到位，要用上条件．
f（x1）-f（x2）=
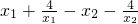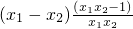=＜0∴函数
在x∈[2，+∞）上是增函数分析：要求用定义证明，则先在给定的区间上任取两个变量，且界大小，再作差变形看符号，若自变量与相应函数值变化一致，则为增函数，若自变量变化与相应函数值变化相反时，则为减函数．
点评：本题主要考查用单调性定义如何来证明函数单调性的，要注意几点：一是自变量的任意性，二是来自相应的区间，三是变形要到位，要用上条件．
练习册系列答案
相关题目
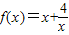在x∈[2，+∞）上是增函数．