题目内容
△ABC中，AB=9，AC=15，∠BAC=120°，它所在平面外一点P到△ABC三个顶点的距离是14，那么点P到平面ABC的距离是： ．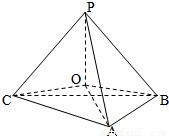
【答案】分析：作出P到平面ABC的高，判断垂足是外心，然后解三角形ABC的外接圆半径，最后求得P到平面ABC的距离．
解答：解析：记P在平面ABC上的射影为O，∵PA=PB=PC
∴OA=OB=OC，即O是△ABC的外心，只需求出OA（△ABC的外接圆的半径），
记为R，在△ABC中由余弦定理知：
BC=21，在由正弦定理知：2R=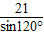
=14
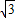，∴OA=7
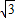，得：PO=7．
故答案为：7．
点评：本题考查棱锥的结构特征，考查正弦定理、余弦定理，是中档题．
解答：解析：记P在平面ABC上的射影为O，∵PA=PB=PC
∴OA=OB=OC，即O是△ABC的外心，只需求出OA（△ABC的外接圆的半径），
记为R，在△ABC中由余弦定理知：
BC=21，在由正弦定理知：2R=
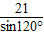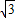=14，∴OA=7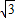，得：PO=7．故答案为：7．
点评：本题考查棱锥的结构特征，考查正弦定理、余弦定理，是中档题．
练习册系列答案
中考解读考点精练系列答案
相关题目
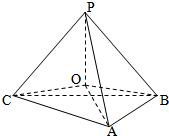△ABC中，AB=9，AC=15，∠BAC=120°，它所在平面外一点P到△ABC三个顶点的距离是14，那么点P到平面ABC的距离是：
如图，△ABC中，AB=9，AC=6，点E在AB上且AE=3，点F在AC上，连接EF，若△AEF与△ABC相似，则AF=
，在AB上取一点E，得到△ADE.若图中的两个三角形相似，则DE的长是（ ）