题目内容
18.(1)△ABC中,a=3$\sqrt{3}$,c=2,B=150°,求b.(2)△ABC中,a=2,b=$\sqrt{2}$,c=$\sqrt{3}$+1,求A.
分析 由余弦定理即可结合已知求值.
解答 (本题满分为12分)
解:(1)∵由余弦定理可得:b2=a2+c2-2accosB=3$\sqrt{3}$2+22-2×3$\sqrt{3}$×2×cos150°=49.
∴解得:b=7.
(2)∵a=2,b=$\sqrt{2}$,c=$\sqrt{3}$+1,
∴由余弦定理可得:cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{2+4+2\sqrt{3}-4}{2×\sqrt{2}×(\sqrt{3}+1)}$=$\frac{\sqrt{2}}{2}$.
∵A∈(0,180°),
∴A=45°.
点评 本题主要考查了余弦定理在解三角形中的应用,考查了计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.函数f(x)=$\sqrt{x}$-x的单调递减区间为( )
| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{1}{4}$)∪$\frac{1}{2}$,+∞) | C. | ($\frac{1}{4}$,+∞) | D. | ($\frac{1}{2}$,+∞) |
6.函数$f(x)=\frac{{2\sqrt{x}}}{x+1}$的最大值为( )
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | 4 |
13.若y=lnx,则其图象在x=2处的切线斜率是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 0 |
3.下列函数在区间(-1,1)上单调递减的是( )
| A. | y=cosx | B. | y=$\frac{1}{x-0.5}$ | C. | y=-ln(x+1) | D. | y=x+$\frac{1}{x}$ |
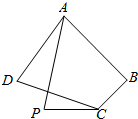 如图,在四边形ABCD中,AB=AD=4,BC=6,CD=2,3$\overrightarrow{AB}$•$\overrightarrow{AD}$+4$\overrightarrow{CB}$•$\overrightarrow{CD}$=0.
如图,在四边形ABCD中,AB=AD=4,BC=6,CD=2,3$\overrightarrow{AB}$•$\overrightarrow{AD}$+4$\overrightarrow{CB}$•$\overrightarrow{CD}$=0.