题目内容
在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.(1)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离;
(2)求(1)中的点N到平面PAC的距离.

【答案】分析:(1)建立空间直角坐标系A-BDP,求出A、B、C、D、P、E的坐标,设出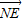 =(-x,
=(-x, ,1-z),利用
,1-z),利用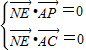 ,求出点N的坐标为(
,求出点N的坐标为(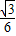 ,0,1),即可得到N到AB、AP的距离分别为1.
,0,1),即可得到N到AB、AP的距离分别为1.
(2)设N到平面PAC的距离为d,通过d=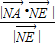 直接求解即可.
直接求解即可.
解答:解:(1)建立空间直角坐标系A-BDP,则A、B、C、D、P、E的坐标分别是A(0,0,0)、B(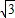 ,0,0)、C(
,0,0)、C(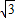 ,1,0)、D(0,1,0)、P(0,0,2)、E(0,
,1,0)、D(0,1,0)、P(0,0,2)、E(0, ,1),依题设N(x,0,z),则
,1),依题设N(x,0,z),则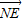 =(-x,
=(-x, ,1-z),由于NE⊥平面PAC,
,1-z),由于NE⊥平面PAC,
∴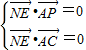
即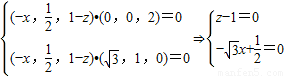
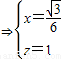 ,
,
即点N的坐标为(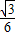 ,0,1),
,0,1),
从而N到AB、AP的距离分别为1.
(2)设N到平面PAC的距离为d,则d=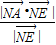
=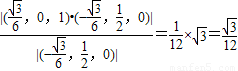 .
.
点评:本题考查空间几何体的两点间的距离的求法,点到平面的距离公式的应用,考查计算能力.
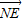 =(-x,
=(-x, ,1-z),利用
,1-z),利用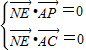 ,求出点N的坐标为(
,求出点N的坐标为(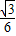 ,0,1),即可得到N到AB、AP的距离分别为1.
,0,1),即可得到N到AB、AP的距离分别为1.(2)设N到平面PAC的距离为d,通过d=
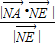 直接求解即可.
直接求解即可.解答:解:(1)建立空间直角坐标系A-BDP,则A、B、C、D、P、E的坐标分别是A(0,0,0)、B(
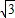 ,0,0)、C(
,0,0)、C(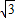 ,1,0)、D(0,1,0)、P(0,0,2)、E(0,
,1,0)、D(0,1,0)、P(0,0,2)、E(0, ,1),依题设N(x,0,z),则
,1),依题设N(x,0,z),则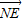 =(-x,
=(-x, ,1-z),由于NE⊥平面PAC,
,1-z),由于NE⊥平面PAC,∴
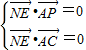
即
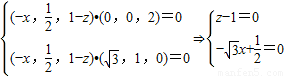
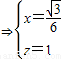 ,
,即点N的坐标为(
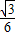 ,0,1),
,0,1),从而N到AB、AP的距离分别为1.
(2)设N到平面PAC的距离为d,则d=
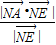
=
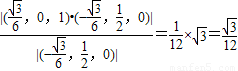 .
.点评:本题考查空间几何体的两点间的距离的求法,点到平面的距离公式的应用,考查计算能力.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2 (2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,
(2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,