题目内容
一个三棱锥的三视图如图所示,其中正视图和侧视图是两条直角边分别是1和2的两个全等的直角三角形,俯视图是直角边长为1的等腰直角三角形.(Ⅰ)请画出这个三棱锥的直观图,并求出它的体积;
(Ⅱ)以D为顶点,DD1,DA,DC为相邻的三条棱,作
平行六面体ABCD-A1B1C1D1,已知点E在AA1上移动
(1)当E点为AA1的中点时,证明BE⊥平面B1C1E.
(2)在CC1上求一点P,使得平面BC1E∥平面PAD1,指出P点的位置
(Ⅲ)AE为何值时,二面角C-ED1-D的大小为45°.

【答案】分析:(Ⅰ)三视图复原几何体是一条侧棱垂直于底面的三棱锥,结合三视图的数据直接求出它的体积;
(Ⅱ)以D为顶点,DD1,DA,DC为相邻的三条棱,作平行六面体ABCD-A1B1C1D1,已知点E在AA1上移动
(1)当E点为AA1的中点时,以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立直角坐标系如图,通过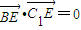 与
与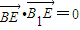 ,证明BE⊥平面B1C1E.
,证明BE⊥平面B1C1E.
(2)在CC1上求一点P,A1E=PC时,有AD1∥BC1使得平面BC1E∥平面PAD1;
(Ⅲ)以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立直角坐标系如图,设E(1,0,m),求出平面C-ED1-D的法向量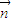 =(2-m,2,1),
=(2-m,2,1), =(0,1,0),利用二面角C-ED1-D的大小为45°求出m值.
=(0,1,0),利用二面角C-ED1-D的大小为45°求出m值.
解答: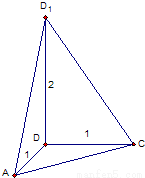 解:(Ⅰ)该三棱锥的直观图是有一条侧棱垂直于底面的三棱锥,
解:(Ⅰ)该三棱锥的直观图是有一条侧棱垂直于底面的三棱锥,
如图所示的三棱锥D1-ACD其中底面ACD是直角边长为1的直角三角形,高DD1=2,故所求的体积是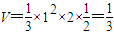 ;
;
(Ⅱ)(1)当E点为AA1的中点时,以D为原点,DA、DC、DD1所在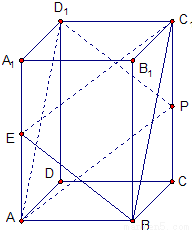 直线分别为x、y、z轴建立直角坐标系如图,则B(1,1,0),B1(1,1,2),C1(0,1,2),E(1,0,1)
直线分别为x、y、z轴建立直角坐标系如图,则B(1,1,0),B1(1,1,2),C1(0,1,2),E(1,0,1)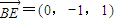 ,
,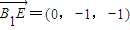 ,
,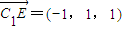
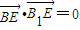 ,
,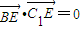
所以BE⊥B1E且BE⊥C1E,所以BE⊥平面B1C1E.
(2)可知当A1E=PC时,有AD1∥BC1,BE∥PD1所以平面BC1E∥平面PAD1
注:也可以求两个平面的法向量,说明两个法向量共线即可.
(Ⅲ)以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立直角坐标系如图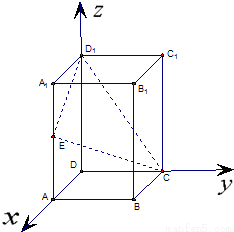
设E(1,0,m)则D(0,0,0),C(0,1,0)D1(0,0,2)
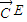 =(1,-1,m),
=(1,-1,m),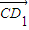 =(0,-1,2)
=(0,-1,2)
设向量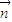 =(x,y,z)满足
=(x,y,z)满足
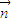 ⊥
⊥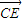 ,
,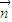 ⊥
⊥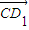
于是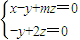 解得
解得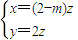
取z=1得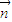 =(2-m,2,1)
=(2-m,2,1)
又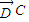 =(0,1,0)
=(0,1,0)
即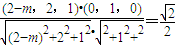
解得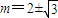
因为m<2所以m=2-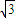
即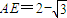 时,二面角C-ED1-D的大小为45°.
时,二面角C-ED1-D的大小为45°.
点评:本题是中档题,考查三视图的知识,三视图还原几何体,直线与平面平行与垂直的证明,二面角的求法,考查转化思想的应用,空间想象能力,计算能力.
(Ⅱ)以D为顶点,DD1,DA,DC为相邻的三条棱,作平行六面体ABCD-A1B1C1D1,已知点E在AA1上移动
(1)当E点为AA1的中点时,以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立直角坐标系如图,通过
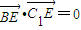 与
与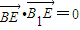 ,证明BE⊥平面B1C1E.
,证明BE⊥平面B1C1E.(2)在CC1上求一点P,A1E=PC时,有AD1∥BC1使得平面BC1E∥平面PAD1;
(Ⅲ)以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立直角坐标系如图,设E(1,0,m),求出平面C-ED1-D的法向量
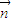 =(2-m,2,1),
=(2-m,2,1), =(0,1,0),利用二面角C-ED1-D的大小为45°求出m值.
=(0,1,0),利用二面角C-ED1-D的大小为45°求出m值.解答:
 解:(Ⅰ)该三棱锥的直观图是有一条侧棱垂直于底面的三棱锥,
解:(Ⅰ)该三棱锥的直观图是有一条侧棱垂直于底面的三棱锥,如图所示的三棱锥D1-ACD其中底面ACD是直角边长为1的直角三角形,高DD1=2,故所求的体积是
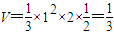 ;
;(Ⅱ)(1)当E点为AA1的中点时,以D为原点,DA、DC、DD1所在
 直线分别为x、y、z轴建立直角坐标系如图,则B(1,1,0),B1(1,1,2),C1(0,1,2),E(1,0,1)
直线分别为x、y、z轴建立直角坐标系如图,则B(1,1,0),B1(1,1,2),C1(0,1,2),E(1,0,1)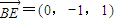 ,
,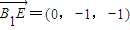 ,
,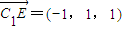
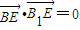 ,
,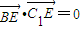
所以BE⊥B1E且BE⊥C1E,所以BE⊥平面B1C1E.
(2)可知当A1E=PC时,有AD1∥BC1,BE∥PD1所以平面BC1E∥平面PAD1
注:也可以求两个平面的法向量,说明两个法向量共线即可.
(Ⅲ)以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立直角坐标系如图

设E(1,0,m)则D(0,0,0),C(0,1,0)D1(0,0,2)
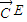 =(1,-1,m),
=(1,-1,m),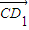 =(0,-1,2)
=(0,-1,2)设向量
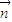 =(x,y,z)满足
=(x,y,z)满足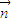 ⊥
⊥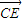 ,
,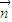 ⊥
⊥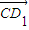
于是
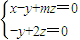 解得
解得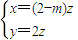
取z=1得
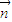 =(2-m,2,1)
=(2-m,2,1)又
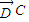 =(0,1,0)
=(0,1,0)即
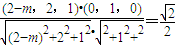
解得
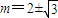
因为m<2所以m=2-
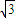
即
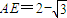 时,二面角C-ED1-D的大小为45°.
时,二面角C-ED1-D的大小为45°.点评:本题是中档题,考查三视图的知识,三视图还原几何体,直线与平面平行与垂直的证明,二面角的求法,考查转化思想的应用,空间想象能力,计算能力.

练习册系列答案
相关题目
 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的体积为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的体积为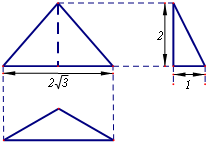 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的外接球体积为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的外接球体积为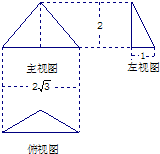 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的体积为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的体积为 (2013•东城区二模)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )
(2013•东城区二模)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )