题目内容
16．若函数f（x）=x+$\frac{1}{x-1}$（x＞1）在x=a处取最小值，则实数a=2．分析 化简f（x）=x+$\frac{1}{x-1}$=x-1+$\frac{1}{x-1}$+1，从而利用基本不等式即可．
解答 解：f（x）=x+$\frac{1}{x-1}$=x-1+$\frac{1}{x-1}$+1
≥2$\sqrt{（x-1）\frac{1}{x-1}}$+1=3，
（当且仅当x-1=$\frac{1}{x-1}$，即x=2时，等号成立），
故a=2；
故答案为：2．
点评 本题考查了学生的化简能力及基本不等式的应用，注意化出定值即可．
练习册系列答案
相关题目
6．已知f（x）=（x-a）（x-b）-2，（a＜b）的两个零点分别为α，β，（α＜β）则（ ）
| A． | a＜α＜b＜β | B． | α＜a＜b＜β | C． | a＜α＜β＜b | D． | α＜a＜β＜b |
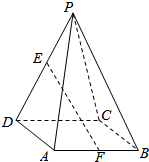如图，四棱锥P-ABCD中，四边形ABCD为平行四边形，E，F分别为所在边中点，证明：EF∥平面PBC．